Linear Equations





Next: Orthogonal Factorizations and
Up: Computational Routines
Previous: Computational Routines
We use the standard notation for a system of simultaneous
linear
equations :
Ax = b
where A is the coefficient matrix,
b is the right hand side,
and x is the solution.
In (2.4) A is assumed to be a square matrix of order n,
but some of the individual routines allow A to be rectangular.
If there are several right hand sides,
we write
AX = B
where the columns of B are the individual right hand sides,
and the columns of
X are the corresponding solutions.
The basic task is to compute X, given A and B.
If A is upper or lower triangular, (2.4) can be solved by a
straightforward
process of backward or forward substitution.
Otherwise, the solution is obtained after first factorizing A as a
product of
triangular matrices (and possibly also a diagonal matrix or permutation
matrix).
The form of the factorization depends on the properties of the matrix
A.
LAPACK provides routines for the following types of matrices, based on
the stated factorizations:
- general matrices (LU factorization with partial pivoting):
A = PLU
where P is a permutation matrix, L is lower triangular with unit
diagonal elements (lower trapezoidal if m > n), and U is upper
triangular (upper trapezoidal if m < n).
- general band matrices including tridiagonal matrices
(LU factorization with partial pivoting):
If A is m-by-m with kl subdiagonals and ku superdiagonals,
the factorization is
A = LU
where L is a product of permutation and unit lower triangular
matrices with kl subdiagonals, and U is upper triangular with
kl + ku superdiagonals.
- symmetric and Hermitian positive definite matrices including
band matrices (Cholesky factorization):
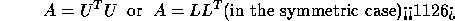
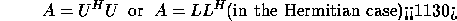
where U is an upper triangular matrix and L is lower triangular.
- symmetric and Hermitian positive definite tridiagonal matrices (
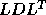 factorization):
factorization): 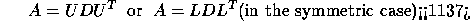
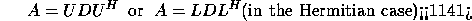
where U is a unit upper bidiagonal matrix, L is unit lower
bidiagonal, and D is diagonal.
- symmetric and Hermitian indefinite matrices (symmetric indefinite
factorization) :
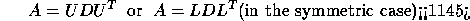
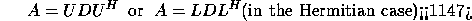
where U (or L) is a product of permutation and unit upper (lower)
triangular matrices, and D is symmetric and block diagonal with diagonal
blocks of order 1 or 2.
The factorization for a general tridiagonal matrix is like that for
a general band matrix with kl = 1 and ku = 1. The factorization
for a symmetric positive definite band matrix with k superdiagonals
(or
subdiagonals) has the same form as for a symmetric positive definite
matrix, but the factor U (or L) is a band matrix with k
superdiagonals (subdiagonals). Band matrices use a compact band
storage scheme described in section 5.3.3.
LAPACK routines are also provided for symmetric matrices (whether
positive definite or indefinite) using packed storage,
as described in section 5.3.2.
While the primary use of a matrix factorization is to solve a system
of equations, other related tasks are provided as well.
Wherever possible, LAPACK provides routines to perform each of these
tasks
for each type of matrix and storage scheme (see
Tables 2.7 and 2.8).
The following list relates the tasks
to the last 3 characters of the name of the corresponding
computational routine:
- xyyTRF:
- factorize (obviously not needed for triangular matrices);
- xyyTRS:
- use the factorization (or the matrix A itself if it is
triangular) to
solve (2.5) by forward or backward substitution;
- xyyCON:
- estimate the reciprocal of the condition number
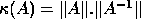 ;
Higham's modification [52] of Hager's method [48]
is used to estimate
;
Higham's modification [52] of Hager's method [48]
is used to estimate 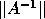 ,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency [50];
,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency [50];
- xyyRFS:
- compute bounds on the error in the computed solution (returned
by the xyyTRS routine), and
refine the solution to reduce the backward error (see below);
- xyyTRI:
- use the factorization (or the matrix A itself if it is
triangular)
to compute
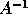 (not provided for band matrices, because the inverse
does not in general preserve bandedness);
(not provided for band matrices, because the inverse
does not in general preserve bandedness);
- xyyEQU:
- compute scaling factors to equilibrate A
(not provided for tridiagonal, symmetric
indefinite, or triangular matrices). These routines do not actually scale
the matrices: auxiliary routines xLAQyy may be used for that purpose -
see the code of the driver routines xyySVX for sample usage .
Note that some of the above routines depend on the output of others:
- xyyTRF:
- may work on an equilibrated matrix produced by
xyyEQU and xLAQyy, if yy is one of {GE, GB, PO, PP, PB};
- xyyTRS:
- requires the factorization returned by xyyTRF;
- xyyCON:
- requires the norm of the original matrix A, and the
factorization returned by xyyTRF;
- xyyRFS:
- requires the original matrices A and B, the factorization
returned by xyyTRF, and the solution X returned by xyyTRS;
- xyyTRI:
- requires the factorization returned by xyyTRF.
The RFS (``refine solution'') routines perform iterative
refinement
and compute backward and forward error bounds for the solution.
Iterative refinement is done in the same precision as the input data.
In particular, the residual is not computed with extra precision,
as has been traditionally done.
The benefit of this procedure is discussed in Section 4.4.
--------------------------------------------------------------------------------
Type of matrix Operation Single precision Double precision
and storage scheme real complex real complex
--------------------------------------------------------------------------------
general factorize SGETRF CGETRF DGETRF ZGETRF
solve using factorization SGETRS CGETRS DGETRS ZGETRS
estimate condition number SGECON CGECON DGECON ZGECON
error bounds for solution SGERFS CGERFS DGERFS ZGERFS
invert using factorization SGETRI CGETRI DGETRI ZGETRI
equilibrate SGEEQU CGEEQU DGEEQU ZGEEQU
--------------------------------------------------------------------------------
general factorize SGBTRF CGBTRF DGBTRF ZGBTRF
band solve using factorization SGBTRS CGBTRS DGBTRS ZGBTRS
estimate condition number SGBCON CGBCON DGBCON ZGBCON
error bounds for solution SGBRFS CGBRFS DGBRFS ZGBRFS
equilibrate SGBEQU CGBEQU DGBEQU ZGBEQU
--------------------------------------------------------------------------------
general factorize SGTTRF CGTTRF DGTTRF ZGTTRF
tridiagonal solve using factorization SGTTRS CGTTRS DGTTRS ZGTTRS
estimate condition number SGTCON CGTCON DGTCON ZGTCON
error bounds for solution SGTRFS CGTRFS DGTRFS ZGTRFS
--------------------------------------------------------------------------------
symmetric/ factorize SPOTRF CPOTRF DPOTRF ZPOTRF
Hermitian solve using factorization SPOTRS CPOTRS DPOTRS ZPOTRS
positive definite estimate condition number SPOCON CPOCON DPOCON ZPOCON
error bounds for solution SPORFS CPORFS DPORFS ZPORFS
invert using factorization SPOTRI CPOTRI DPOTRI ZPOTRI
equilibrate SPOEQU CPOEQU DPOEQU ZPOEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPPTRF CPPTRF DPPTRF ZPPTRF
Hermitian solve using factorization SPPTRS CPPTRS DPPTRS ZPPTRS
positive definite estimate condition number SPPCON CPPCON DPPCON ZPPCON
(packed storage) error bounds for solution SPPRFS CPPRFS DPPRFS ZPPRFS
invert using factorization SPPTRI CPPTRI DPPTRI ZPPTRI
equilibrate SPPEQU CPPEQU DPPEQU ZPPEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPBTRF CPBTRF DPBTRF ZPBTRF
Hermitian solve using factorization SPBTRS CPBTRS DPBTRS ZPBTRS
positive definite estimate condition number SPBCON CPBCON DPBCON ZPBCON
band error bounds for solution SPBRFS CPBRFS DPBRFS ZPBRFS
equilibrate SPBEQU CPBEQU DPBEQU ZPBEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPTTRF CPTTRF DPTTRF ZPTTRF
Hermitian solve using factorization SPTTRS CPTTRS DPTTRS ZPTTRS
positive definite estimate condition number SPTCON CPTCON DPTCON ZPTCON
tridiagonal error bounds for solution SPTRFS CPTRFS DPTRFS ZPTRFS
--------------------------------------------------------------------------------
Table 2.7: Computational routines for linear equations
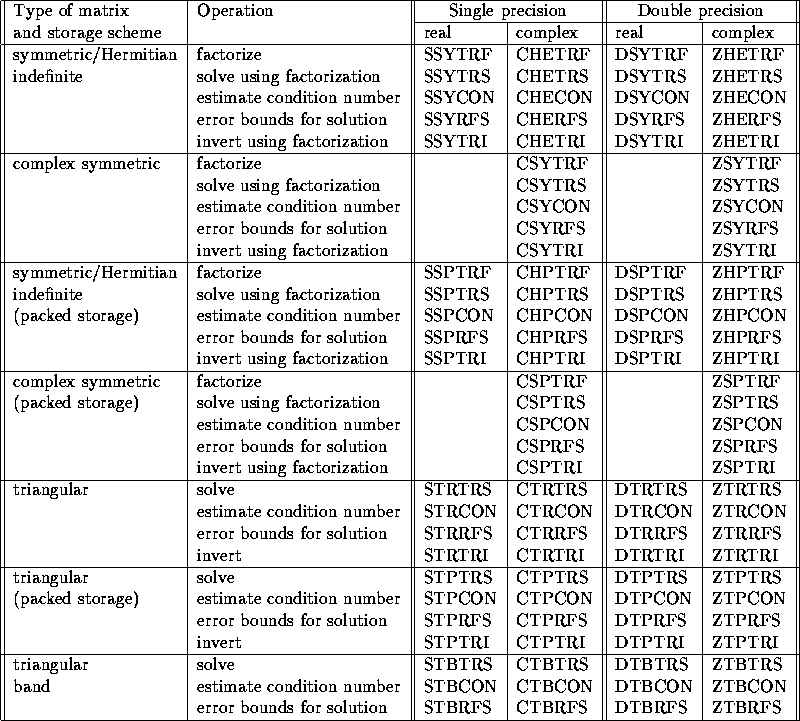
Table 2.8: Computational routines for linear equations (continued)





Next: Orthogonal Factorizations and
Up: Computational Routines
Previous: Computational Routines
Tue Nov 29 14:03:33 EST 1994
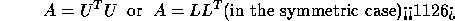
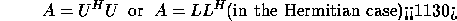
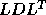 factorization):
factorization): 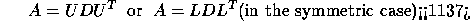
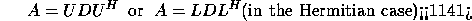
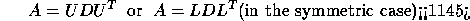
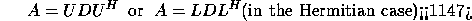
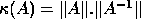 ;
Higham's modification [52] of Hager's method [48]
is used to estimate
;
Higham's modification [52] of Hager's method [48]
is used to estimate 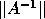 ,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency [50];
,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency [50];
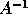 (not provided for band matrices, because the inverse
does not in general preserve bandedness);
(not provided for band matrices, because the inverse
does not in general preserve bandedness);
