Error Bounds for Linear Equation Solving

Let Ax = b be the system to be solved, and the computed solution. Let n be the dimension of A. An approximate error bound  for may be obtained in one of the following two ways, depending on whether the solution is computed by a simple driver or an expert driver:

1. Suppose that Ax = b is solved using the simple driver SGESV   (subsection 2.2.1). Then the approximate error bound

   

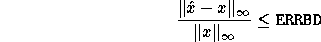
   can be computed by the following code fragment.

      EPSMCH = SLAMCH( 'E' )
   *  Get infinity-norm of A
      ANORM = SLANGE( 'I', N, N, A, LDA, WORK )
   *  Solve system; The solution X overwrites B
      CALL SGESV( N, 1, A, LDA, IPIV, B, LDB, INFO )
      IF( INFO.GT.0 ) THEN
         PRINT *,'Singular Matrix'
      ELSE IF (N .GT. 0) THEN
   *     Get reciprocal condition number RCOND of A
         CALL SGECON( 'I', N, A, LDA, ANORM, RCOND,
   $                  WORK, IWORK, INFO )
         RCOND = MAX( RCOND, EPSMCH )
         ERRBD = EPSMCH / RCOND
      END IF
   

    

   For example, suppose

   ,

   

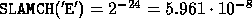   Then (to 4 decimal places)

   

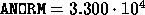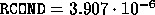   , , the true reciprocal condition number 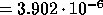, , 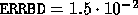and the true error .  

2. Suppose that Ax = b is solved using the expert driver SGESVX (subsection 2.2.1).   This routine provides an explicit error bound FERR, measured with the infinity-norm:  

   

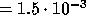   For example, the following code fragment solves Ax = b and computes an approximate error bound FERR:

         CALL SGESVX( 'E', 'N', N, 1, A, LDA, AF, LDAF, IPIV,
   $          EQUED, R, C, B, LDB, X, LDX, RCOND, FERR, BERR,
   $          WORK, IWORK, INFO )
         IF( INFO.GT.0 ) PRINT *,'(Nearly) Singular Matrix'
   

   For the same A and b as above, 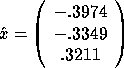, , and the actual error is .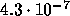

This example illustrates that the expert driver provides an error bound with less programming effort than the simple driver, and also that it may produce a significantly more accurate answer.

Similar code fragments, with obvious adaptations, may be used with all the driver routines for linear equations listed in Table 2.2. For example, if a symmetric system is solved using the simple driver xSYSV, then xLANSY must be used to compute ANORM, and xSYCON must be used to compute RCOND.

• Further Details: Error Bounds for Linear Equation Solving