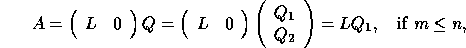
The LQ factorization is given by
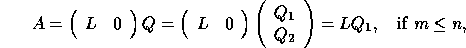
where L is m-by-m lower triangular, Q is n-by-n
orthogonal (or unitary), 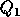 consists of the first m rows of Q,
and
consists of the first m rows of Q,
and 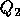 the remaining n - m rows.
the remaining n - m rows.
This factorization is computed by the routine xGELQF, and again Q is
represented as a product of elementary reflectors; xORGLQ
(or xUNGLQ in the complex case) can generate
all or part of Q, and xORMLQ (or xUNMLQ
) can pre- or post-multiply a given
matrix
by Q or 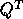 (
(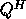 if Q is complex).
if Q is complex).
The LQ factorization of A is essentially the same as the QR factorization
of 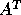 (
(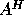 if A is complex), since
if A is complex), since

The LQ factorization may be used to find a minimum norm solution of an underdetermined system of linear equations Ax = b where A is m-by-n with m < n and has rank m. The solution is given by

and may be computed by calls to xTRTRS and xORMLQ.