Singular Value Decomposition





Next: Generalized Symmetric Definite
Up: Computational Routines
Previous: Invariant Subspaces and
Let A be a general real m-by-n matrix. The singular value
decomposition (SVD) of A is the factorization 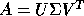 , where
U and V are orthogonal, and
, where
U and V are orthogonal, and
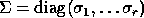 , r = min(m , n),
with
, r = min(m , n),
with  . If A is complex, then
its SVD is
. If A is complex, then
its SVD is 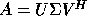 where U and V are unitary,
and
where U and V are unitary,
and  is as before with real
diagonal elements.
The
is as before with real
diagonal elements.
The 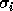 are called the singular values ,
the first r columns of V
the right singular vectors and
the first r columns of U
the left singular vectors .
are called the singular values ,
the first r columns of V
the right singular vectors and
the first r columns of U
the left singular vectors .
The routines described in this section, and listed in Table 2.12,
are used to compute this decomposition.
The computation proceeds in the following stages:
- The matrix A is reduced to bidiagonal
form:
 if
A is real (
if
A is real (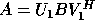 if A is complex), where
if A is complex), where 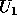 and
and  are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
- The SVD of the bidiagonal matrix B is computed:
 ,
where
,
where 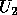 and
and 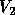 are orthogonal and
are orthogonal and  is diagonal as described
above. The singular vectors of A are then
is diagonal as described
above. The singular vectors of A are then 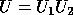 and
and
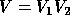 .
.
The reduction to bidiagonal form is performed by the subroutine xGEBRD,
or by xGBBRD
for a band matrix.
The routine xGEBRD represents
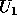 and
and  in factored form as products of elementary reflectors,
as described in section 5.4.
If A is real,
the matrices
in factored form as products of elementary reflectors,
as described in section 5.4.
If A is real,
the matrices 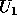 and
and  may be computed explicitly using routine xORGBR,
or multiplied by other matrices without forming
may be computed explicitly using routine xORGBR,
or multiplied by other matrices without forming 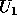 and
and  using routine xORMBR .
If A is complex, one instead uses xUNGBR
and xUNMBR , respectively.
using routine xORMBR .
If A is complex, one instead uses xUNGBR
and xUNMBR , respectively.
If A is banded and xGBBRD is used to reduce it to bidiagonal form,
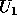 and
and  are determined as products of Givens rotations
, rather than
as products of elementary reflectors. If
are determined as products of Givens rotations
, rather than
as products of elementary reflectors. If 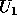 or
or  is required, it
must be formed explicitly by xGBBRD. xGBBRD uses a vectorizable
algorithm, similar to that used by xSBTRD (see Kaufman [57]).
xGBBRD may be much faster than xGEBRD when the bandwidth is narrow.
is required, it
must be formed explicitly by xGBBRD. xGBBRD uses a vectorizable
algorithm, similar to that used by xSBTRD (see Kaufman [57]).
xGBBRD may be much faster than xGEBRD when the bandwidth is narrow.
The SVD of the bidiagonal matrix is computed by the subroutine xBDSQR.
xBDSQR is more accurate than its counterparts in LINPACK and EISPACK:
barring underflow and overflow, it computes all the singular values of
A to nearly full relative precision, independent of their magnitudes.
It also computes the singular vectors much more accurately. See
section 4.9 and
[41][16][22] for details.
If m >> n, it may be more efficient to first perform a QR factorization
of A, using the routine xGEQRF
,
and then to compute the SVD of the n-by-n matrix R, since
if A = QR and 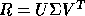 , then the SVD of A is given by
, then the SVD of A is given by
 .
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
factorizations are performed by the driver xGESVD.
.
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
factorizations are performed by the driver xGESVD.
The SVD may be used to find a minimum norm solution to a (possibly)
rank-deficient linear least squares
problem (2.1). The effective rank, k, of A can be determined as the
number of singular values which exceed a suitable threshold.
Let  be the leading k-by-k submatrix of
be the leading k-by-k submatrix of  , and
, and
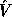 be the matrix consisting of the first k columns of V.
Then the solution is given by:
be the matrix consisting of the first k columns of V.
Then the solution is given by:

where 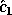 consists of the first k elements of
consists of the first k elements of 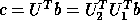 .
. 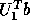 can be computed using xORMBR, and
xBDSQR has an option to multiply a vector by
can be computed using xORMBR, and
xBDSQR has an option to multiply a vector by 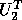 .
.
-----------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
-----------------------------------------------------------------------------
general bidiagonal reduction SGEBRD CGEBRD DGEBRD ZGEBRD
-----------------------------------------------------------------------------
general band bidiagonal reduction SGBBRD CGBBRD DGBBRD ZGBBRD
-----------------------------------------------------------------------------
orthogonal/unitary generate matrix after SORGBR CUNGBR DORGBR ZUNGBR
bidiagonal reduction
multiply matrix after SORMBR CUNMBR DORMBR ZUNMBR
bidiagonal reduction
-----------------------------------------------------------------------------
bidiagonal singular values/ SBDSQR CBDSQR DBDSQR ZBDSQR
singular vectors
-----------------------------------------------------------------------------
Table 2.12: Computational routines for the singular value decomposition





Next: Generalized Symmetric Definite
Up: Computational Routines
Previous: Invariant Subspaces and
Tue Nov 29 14:03:33 EST 1994
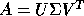 , where
U and V are orthogonal, and
, where
U and V are orthogonal, and
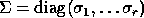 , r = min(m , n),
with
, r = min(m , n),
with  . If A is complex, then
its SVD is
. If A is complex, then
its SVD is 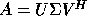 where U and V are unitary,
and
where U and V are unitary,
and  is as before with real
diagonal elements.
The
is as before with real
diagonal elements.
The 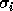 are called the singular values ,
the first r columns of V
the right singular vectors and
the first r columns of U
the left singular vectors .
are called the singular values ,
the first r columns of V
the right singular vectors and
the first r columns of U
the left singular vectors .
 if
A is real (
if
A is real (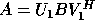 if A is complex), where
if A is complex), where 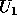 and
and  are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
 ,
where
,
where 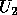 and
and 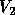 are orthogonal and
are orthogonal and 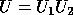 and
and
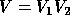 .
.
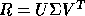 , then the SVD of A is given by
, then the SVD of A is given by
 .
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
.
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
 be the leading k-by-k submatrix of
be the leading k-by-k submatrix of 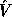 be the matrix consisting of the first k columns of V.
Then the solution is given by:
be the matrix consisting of the first k columns of V.
Then the solution is given by:
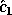 consists of the first k elements of
consists of the first k elements of 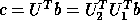 .
. 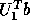 can be computed using xORMBR, and
can be computed using xORMBR, and
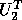 .
.