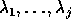 ,
, 1 < = j < = n, appear in the upper left corner of T. Then the first j columns of Z span the right invariant subspace of A corresponding to
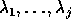 .
.
The Schur form depends on the order of the eigenvalues on the diagonal
of T and this may optionally be chosen by the user. Suppose the user chooses
that 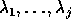 ,
,
1 < = j < = n, appear in the upper left
corner of T. Then the first j columns of Z span the right invariant
subspace of A corresponding to 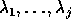 .
.
The following routines perform this re-ordering and also compute condition numbers for eigenvalues, eigenvectors, and invariant subspaces:
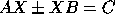 for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
See Table 2.11 for a complete list of the routines.
-----------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
-----------------------------------------------------------------------------
general Hessenberg reduction SGEHRD CGEHRD DGEHRD ZGEHRD
balancing SGEBAL CGEBAL DGEBAL ZGEBAL
backtransforming SGEBAK CGEBAK DGEBAK ZGEBAK
-----------------------------------------------------------------------------
orthogonal/unitary generate matrix after SORGHR CUNGHR DORGHR ZUNGHR
Hessenberg reduction
multiply matrix after SORMHR CUNMHR DORMHR ZUNMHR
Hessenberg reduction
-----------------------------------------------------------------------------
Hessenberg Schur factorization SHSEQR CHSEQR DHSEQR ZHSEQR
eigenvectors by SHSEIN CHSEIN DHSEIN ZHSEIN
inverse iteration
-----------------------------------------------------------------------------
(quasi)triangular eigenvectors STREVC CTREVC DTREVC ZTREVC
reordering Schur STREXC CTREXC DTREXC ZTREXC
factorization
Sylvester equation STRSYL CTRSYL DTRSYL ZTRSYL
condition numbers of STRSNA CTRSNA DTRSNA ZTRSNA
eigenvalues/vectors
condition numbers of STRSEN CTRSEN DTRSEN ZTRSEN
eigenvalue cluster/
invariant subspace
-----------------------------------------------------------------------------
Table 2.11: Computational routines for the nonsymmetric eigenproblem