




Next: Shifted QEP.
Up: Spectral Transformations for QEP
Previous: Spectral Transformations for QEP
Contents
Index
For most iterative methods for solving a generalized eigenvalue problem,
the formulation (9.4), with either (9.5) or with
(9.10), is suitable if one wants to determine a few
of the exterior eigenvalues and eigenvectors. If one wants to compute
some of the smallest (in modulus) eigenvalues and eigenvectors, then the
obvious transformation is 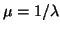 , and, after multiplying
the QEP (9.1) with
, and, after multiplying
the QEP (9.1) with 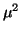 , we obtain the invert QEP:
, we obtain the invert QEP:
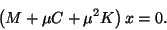 |
(256) |
Here it is assumed that 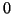 is not an eigenvalue of the
original QEP (9.1), i.e., that
is not an eigenvalue of the
original QEP (9.1), i.e., that 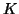 is nonsingular.
is nonsingular.
The QEP for the triplet 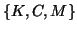 can be linearized as discussed
in §9.2.2,
for instance, as (9.4) with (9.5), where
can be linearized as discussed
in §9.2.2,
for instance, as (9.4) with (9.5), where 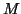 interchanged with
interchanged with 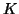 . We can reformulate this generalized
linearized eigenproblem in terms of
. We can reformulate this generalized
linearized eigenproblem in terms of  , instead of
, instead of 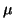 ,
which leads to
,
which leads to
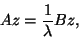 |
(257) |
where
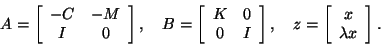 |
(258) |
Note that from the factorization
we know that the pencil 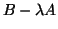 is equivalent to
is equivalent to
Since
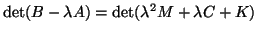 ,
we conclude that the matrix pencil
,
we conclude that the matrix pencil 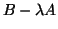 is regular if
and only if
the quadratic matrix polynomial
is regular if
and only if
the quadratic matrix polynomial
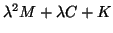 is regular and the eigenvalues of the original QEP (9.1)
coincide with the eigenvalues of the matrix pencil
is regular and the eigenvalues of the original QEP (9.1)
coincide with the eigenvalues of the matrix pencil 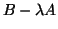 .
.
For the special case (9.2), we may formulate the
generalized eigenvalue problem
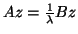 , with
, with
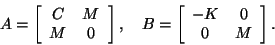 |
(259) |
In this case, both matrices are Hermitian, but indefinite.
Linearization with (9.15) results after left
multiplication of (9.14) with a block-diagonal
matrix
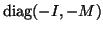 . Therefore, if
. Therefore, if
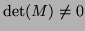 , then the pencil
, then the pencil 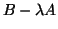 is regular if and
only if
the quadratic matrix polynomial
is regular if and
only if
the quadratic matrix polynomial
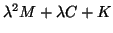 is regular.
is regular.





Next: Shifted QEP.
Up: Spectral Transformations for QEP
Previous: Spectral Transformations for QEP
Contents
Index
Susan Blackford
2000-11-20
![]() can be linearized as discussed
in §9.2.2,
for instance, as (9.4) with (9.5), where
can be linearized as discussed
in §9.2.2,
for instance, as (9.4) with (9.5), where ![]() interchanged with
interchanged with ![]() . We can reformulate this generalized
linearized eigenproblem in terms of
. We can reformulate this generalized
linearized eigenproblem in terms of ![]() , instead of
, instead of ![]() ,
which leads to
,
which leads to
![]() , with
, with