




Next: Spectral Transformations for QEP
Up: Quadratic Eigenvalue Problems Z. Bai,
Previous: Introduction
Contents
Index
Transformation to Linear Form
It is easy to see that the QEP in (9.1) is equivalent to
the following generalized
``linear'' eigenvalue problem:![[*]](http://www.netlib.org/utk/icons/footnote.png)
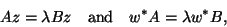 |
(248) |
where
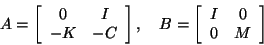 |
(249) |
and
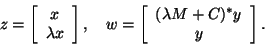 |
(250) |
The generalized eigenvalue problem (9.4)
is commonly called a linearization of the QEP (9.1).
It can be shown that for any matrices  and
and  of the above forms,
the right and left eigenvectors
of the above forms,
the right and left eigenvectors 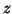 and
and 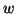 have the structures
described in (9.6).
have the structures
described in (9.6).
Note that from the factorization
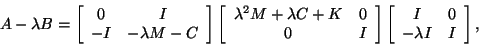 |
(251) |
we can conclude that the pencil 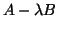 is equivalent
is equivalent![[*]](http://www.netlib.org/utk/icons/footnote.png) to the matrix
to the matrix
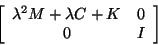 |
(252) |
and
This means that the eigenvalues of the original QEP (9.1)
coincide with the eigenvalues of the generalized eigenvalue
problem (9.4). Furthermore, we have that
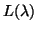 is regular if and only if
is regular if and only if 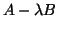 is regular;
is regular;
- if
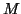 (hence
(hence  ) is nonsingular, then
) is nonsingular, then 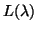 is regular;
is regular;
- if
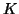 (hence
(hence  ) is nonsingular, then
) is nonsingular, then 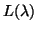 is regular.
is regular.
For the theory on regular pencils 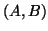 , see, for instance,
[425, Chap. VI].
We will assume that at least
, see, for instance,
[425, Chap. VI].
We will assume that at least 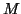 is nonsingular throughout this section.
is nonsingular throughout this section.
A disadvantage of the above reduction to linear form is that if
the matrices 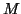 ,
, 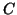 , and
, and 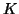 are all Hermitian, then this is not reflected in
the reduced form (9.5), where
are all Hermitian, then this is not reflected in
the reduced form (9.5), where  is
non-Hermitian. This can be repaired as follows.
is
non-Hermitian. This can be repaired as follows.
In fact, the matrix pair 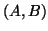 in (9.4) can be
chosen in a more general form
in (9.4) can be
chosen in a more general form
where 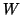 can be any arbitrary nonsingular matrix.
Note that now the matrix pencil
can be any arbitrary nonsingular matrix.
Note that now the matrix pencil 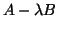 is equivalent to the
matrix polynomial (9.8) if and only if
is equivalent to the
matrix polynomial (9.8) if and only if 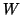 is nonsingular,
and because of (9.7),
is nonsingular,
and because of (9.7),
For example, if the matrices 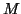 ,
, 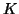 , and
, and 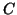 are all symmetric, as
in the special case (9.2), and
are all symmetric, as
in the special case (9.2), and 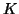 is nonsingular, then we may choose
is nonsingular, then we may choose
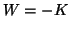 , which leads to the following symmetric generalized ``linear''
eigenvalue problem
, which leads to the following symmetric generalized ``linear''
eigenvalue problem
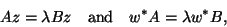 |
(253) |
where
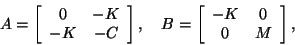 |
(254) |
and
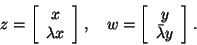 |
(255) |
Both  and
and  are symmetric, but may be indefinite.
are symmetric, but may be indefinite.





Next: Spectral Transformations for QEP
Up: Quadratic Eigenvalue Problems Z. Bai,
Previous: Introduction
Contents
Index
Susan Blackford
2000-11-20
![]() ,
, ![]() , and
, and ![]() are all Hermitian, then this is not reflected in
the reduced form (9.5), where
are all Hermitian, then this is not reflected in
the reduced form (9.5), where ![]() is
non-Hermitian. This can be repaired as follows.
is
non-Hermitian. This can be repaired as follows.
![]() in (9.4) can be
chosen in a more general form
in (9.4) can be
chosen in a more general form