




Next: Algorithm
Up: Deflation and Restart
Previous: Deflation.
Contents
Index
Suppose that the generalized Schur form (8.12) is
ordered with respect to 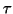 such that
such that
where 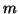 is the dimension of
is the dimension of
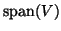 . Then, for
. Then, for 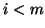 , the
space
, the
space
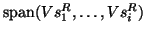 spanned by the first
spanned by the first 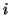 columns
of
columns
of 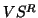 contains the
contains the 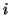 most promising Petrov vectors.
The corresponding test subspace is given by
most promising Petrov vectors.
The corresponding test subspace is given by
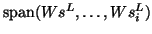 .
Therefore, in order to reduce the dimension of the subspaces (``implicit
restart'') to
.
Therefore, in order to reduce the dimension of the subspaces (``implicit
restart'') to 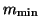 ,
,
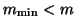 , the columns
, the columns
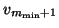 through
through 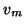 and
and
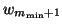 through
through 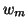 can simply be discarded
and the Jacobi-Davidson algorithm can be continued with
can simply be discarded
and the Jacobi-Davidson algorithm can be continued with
Susan Blackford
2000-11-20