




Next: Restart.
Up: Deflation and Restart
Previous: Deflation and Restart
Contents
Index
The partial generalized Schur form
can be obtained in a number of successive
steps. Suppose that we have the partial
generalized Schur form
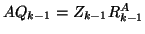 and
and
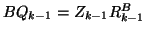 . We want to
expand this partial generalized Schur form
with the new right Schur vector
. We want to
expand this partial generalized Schur form
with the new right Schur vector 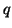 and the left Schur vector
and the left Schur vector 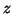 to
to
and
The new generalized Schur pair
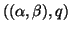 satisfies
satisfies
or, since
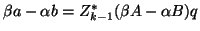 ,
,
The vectors 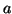 and
and 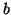 can be computed from
can be computed from
Hence, the generalized Schur pair
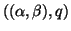 is an
eigenpair of the deflated matrix pair
is an
eigenpair of the deflated matrix pair
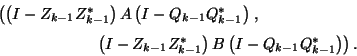 |
(228) |
This eigenproblem can be solved again with the
Jacobi-Davidson process that we have outlined in §8.4.1.
In that process we construct vectors  that are orthogonal to
that are orthogonal to  and vectors
and vectors 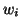 that are orthogonal to
that are orthogonal to 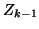 . This simplifies the
computation of the interaction matrices
. This simplifies the
computation of the interaction matrices 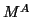 and
and 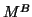 , associated with the
deflated operators:
, associated with the
deflated operators:
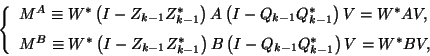 |
(229) |
and 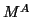 and
and 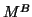 can be simply computed as
can be simply computed as 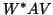 and
and 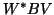 ,
respectively.
,
respectively.





Next: Restart.
Up: Deflation and Restart
Previous: Deflation and Restart
Contents
Index
Susan Blackford
2000-11-20