| (80) |
The basic recursion (5.9) is replaced by
The matrix ![]() is symmetric,
is symmetric,
An eigensolution of ![]() ,
,
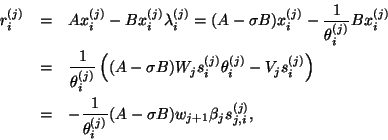
As in the standard case, we can
monitor
![]() and flag the eigenvalue
and flag the eigenvalue ![]() as converged when it gets small,
without actually performing the matrix-vector
multiplication (5.20). We save this
operation until the step
as converged when it gets small,
without actually performing the matrix-vector
multiplication (5.20). We save this
operation until the step ![]() when the estimate
indicates convergence.
when the estimate
indicates convergence.
We get the following algorithm.
We note that only a few steps differ from the previous direct iteration algorithm. In actual implementations one can use the same program for both computations. Let us comment on those steps that differ:
We may save and use the auxiliary basis ![]() to save extra
to save extra ![]() operations,
operations,
When we run a shift-and-invert operator (5.16),
we factor
During the actual iteration, we use the factors ![]() and
and ![]() ,
computing
,
computing
If there are eigenvalues ![]() on both sides of the shift
on both sides of the shift ![]() ,
the matrix
,
the matrix ![]() is indefinite, and we cannot use simple Cholesky
decomposition, but have to make a symmetric indefinite
factorization, e.g., MA47 of Duff and Reid [141].
See §10.3.
This type of algorithm makes
is indefinite, and we cannot use simple Cholesky
decomposition, but have to make a symmetric indefinite
factorization, e.g., MA47 of Duff and Reid [141].
See §10.3.
This type of algorithm makes ![]() block-diagonal with one by one
and two by two blocks. It is easy to determine the inertia
of such a matrix, and this gives information on exactly how
many eigenvalues there are on each side of the shift
block-diagonal with one by one
and two by two blocks. It is easy to determine the inertia
of such a matrix, and this gives information on exactly how
many eigenvalues there are on each side of the shift ![]() .
We may determine the number of eigenvalues in an interval
by performing two factorizations with
.
We may determine the number of eigenvalues in an interval
by performing two factorizations with ![]() in either end
point. This is used to make sure that all eigenvalues in the
interval have been computed in the software based on [162] and
[206].
in either end
point. This is used to make sure that all eigenvalues in the
interval have been computed in the software based on [162] and
[206].
We note that Algorithm 5.5 does not need any
factorization of the matrix ![]() and can be applied also when
and can be applied also when ![]() is
singular. This is not an uncommon case in practical situations,
but special precautions have to be taken to prevent components of
the null space of
is
singular. This is not an uncommon case in practical situations,
but special precautions have to be taken to prevent components of
the null space of ![]() from entering the computation; see [161] or
[340].
from entering the computation; see [161] or
[340].