




Next: Overview of Available Algorithms.
Up: Generalized Hermitian Eigenvalue Problems
Previous: Generalized Hermitian Eigenvalue Problems
Contents
Index
A generalized Hermitian eigenvalue problem (GHEP) is given by
 |
(66) |
where  and
and  are Hermitian,
are Hermitian, 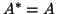 , and
, and 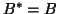 .
We call the pair
.
We call the pair 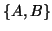 of matrices in (5.1)
a matrix pencil.
In this chapter we make the additional assumption that
of matrices in (5.1)
a matrix pencil.
In this chapter we make the additional assumption that
 or
or  or
or
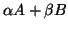 for some scalars
for some scalars 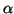 and
and 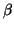 is positive definite, in which case we talk about a
Hermitian definite pencil.
This assumption is true for a wide class of practically
important cases, and the theory is very closely related to the
standard Hermitian eigenproblem, as expounded in Chapter 4.
If no positive definite combination exists, we could as well regard
is positive definite, in which case we talk about a
Hermitian definite pencil.
This assumption is true for a wide class of practically
important cases, and the theory is very closely related to the
standard Hermitian eigenproblem, as expounded in Chapter 4.
If no positive definite combination exists, we could as well regard
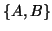 as a general pencil and use the theory and algorithms described
in Chapter 8.
as a general pencil and use the theory and algorithms described
in Chapter 8.
The nonstandard case, where
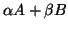 is positive definite,
may be reduced to the standard case when
is positive definite,
may be reduced to the standard case when  is positive definite,
by noting that the pencil
is positive definite,
by noting that the pencil
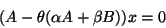 |
(67) |
has eigenvalues
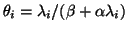 and the same eigenvectors
as the original pencil (5.1).
One may apply any algorithm applicable
for positive definite
and the same eigenvectors
as the original pencil (5.1).
One may apply any algorithm applicable
for positive definite  to this modified pencil and recover the
to this modified pencil and recover the
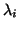 from the
from the 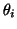 .
.
The GHEP (5.1) has  real eigenvalues
real eigenvalues
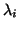 , which we may order increasingly so that
, which we may order increasingly so that
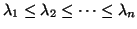 . Several
eigenvalues may coincide, as in the standard case,
except that some eigenvalues
may be infinite. If the matrices
. Several
eigenvalues may coincide, as in the standard case,
except that some eigenvalues
may be infinite. If the matrices  and
and  are
positive definite,
are
positive definite, 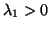 , but if
, but if  is positive semidefinite
we can only say that
is positive semidefinite
we can only say that
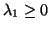 .
.
When the pencil 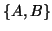 is Hermitian definite,
it is possible to find
is Hermitian definite,
it is possible to find  mutually
mutually
 -orthogonal eigenvectors,
-orthogonal eigenvectors,
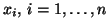 , so that
, so that
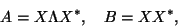 |
(68) |
where
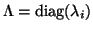 and
and
![$X=[x_1,x_2,\dots,x_n]$](img758.png) .
The eigenvectors
.
The eigenvectors 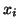 are not unique, but there is a unique
reducing subspace for each different eigenvalue.
For a Hermitian definite pencil, the reducing subspace
is of the same dimension
as the multiplicity of the eigenvalue. It is important to keep in mind that
when a couple of eigenvalues coincide, their eigenvectors lose
their individuality: there is no way of saying that one set of vectors
comprises the eigenvectors of a multiple eigenvalue.
are not unique, but there is a unique
reducing subspace for each different eigenvalue.
For a Hermitian definite pencil, the reducing subspace
is of the same dimension
as the multiplicity of the eigenvalue. It is important to keep in mind that
when a couple of eigenvalues coincide, their eigenvectors lose
their individuality: there is no way of saying that one set of vectors
comprises the eigenvectors of a multiple eigenvalue.
There are some cases where the matrix  is singular (positive
semidefinite). We still have a Hermitian definite pencil provided
that
is singular (positive
semidefinite). We still have a Hermitian definite pencil provided
that 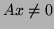 for all vectors
for all vectors 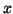 in the null space of
in the null space of  . The
pencil (5.1) then has a
. The
pencil (5.1) then has a 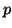 -fold infinite eigenvalue with
the null space of
-fold infinite eigenvalue with
the null space of  as its reducing subspace. In most practical
cases, we are not interested in computing these infinite eigenvalues,
since they correspond to constraints, symmetries or rigid body modes of the
physical application that gave rise to the eigenvalue computation.
as its reducing subspace. In most practical
cases, we are not interested in computing these infinite eigenvalues,
since they correspond to constraints, symmetries or rigid body modes of the
physical application that gave rise to the eigenvalue computation.
Eigenvalues 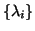 of
of 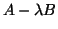 may be well-conditioned
or ill-conditioned. If
may be well-conditioned
or ill-conditioned. If 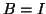 (or close to it), the eigenvalues
are well-conditioned (close to it) as for the Hermitian eigenproblem.
But if
(or close to it), the eigenvalues
are well-conditioned (close to it) as for the Hermitian eigenproblem.
But if
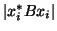 is small, where
is small, where 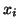 is a unit
eigenvector of
is a unit
eigenvector of 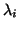 ,
,  can be very
ill-conditioned. We give a more detailed account of error assessment
for the computed eigenvalues and eigenvectors in §5.7.
can be very
ill-conditioned. We give a more detailed account of error assessment
for the computed eigenvalues and eigenvectors in §5.7.
Subsections





Next: Overview of Available Algorithms.
Up: Generalized Hermitian Eigenvalue Problems
Previous: Generalized Hermitian Eigenvalue Problems
Contents
Index
Susan Blackford
2000-11-20
![]() is positive definite,
may be reduced to the standard case when
is positive definite,
may be reduced to the standard case when ![]() is positive definite,
by noting that the pencil
is positive definite,
by noting that the pencil
![]() real eigenvalues
real eigenvalues
![]() , which we may order increasingly so that
, which we may order increasingly so that
![]() . Several
eigenvalues may coincide, as in the standard case,
except that some eigenvalues
may be infinite. If the matrices
. Several
eigenvalues may coincide, as in the standard case,
except that some eigenvalues
may be infinite. If the matrices ![]() and
and ![]() are
positive definite,
are
positive definite, ![]() , but if
, but if ![]() is positive semidefinite
we can only say that
is positive semidefinite
we can only say that
![]() .
.
![]() is Hermitian definite,
it is possible to find
is Hermitian definite,
it is possible to find ![]() mutually
mutually
![]() -orthogonal eigenvectors,
-orthogonal eigenvectors,
![]() , so that
, so that
![]() is singular (positive
semidefinite). We still have a Hermitian definite pencil provided
that
is singular (positive
semidefinite). We still have a Hermitian definite pencil provided
that ![]() for all vectors
for all vectors ![]() in the null space of
in the null space of ![]() . The
pencil (5.1) then has a
. The
pencil (5.1) then has a ![]() -fold infinite eigenvalue with
the null space of
-fold infinite eigenvalue with
the null space of ![]() as its reducing subspace. In most practical
cases, we are not interested in computing these infinite eigenvalues,
since they correspond to constraints, symmetries or rigid body modes of the
physical application that gave rise to the eigenvalue computation.
as its reducing subspace. In most practical
cases, we are not interested in computing these infinite eigenvalues,
since they correspond to constraints, symmetries or rigid body modes of the
physical application that gave rise to the eigenvalue computation.
![]() of
of ![]() may be well-conditioned
or ill-conditioned. If
may be well-conditioned
or ill-conditioned. If ![]() (or close to it), the eigenvalues
are well-conditioned (close to it) as for the Hermitian eigenproblem.
But if
(or close to it), the eigenvalues
are well-conditioned (close to it) as for the Hermitian eigenproblem.
But if
![]() is small, where
is small, where ![]() is a unit
eigenvector of
is a unit
eigenvector of ![]() ,
, ![]() can be very
ill-conditioned. We give a more detailed account of error assessment
for the computed eigenvalues and eigenvectors in §5.7.
can be very
ill-conditioned. We give a more detailed account of error assessment
for the computed eigenvalues and eigenvectors in §5.7.