




Next: Transformation to Standard Problem
Up: Introduction
Previous: Eigenvalues Sought.
Contents
Index
In the final columns of Table 5.1,
we give an estimate of storage needed and extra work for factorizations.
- ``#vec''
- gives how many vectors one needs to store.
The meaning of 2 is obvious;
``Moderate'' means a multiple of the number
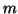 of eigenvalues sought, say
of eigenvalues sought, say 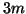 to
to 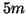 . ``Few'' is smaller than
moderate, say
. ``Few'' is smaller than
moderate, say 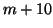 , and ``Many'' is larger.
, and ``Many'' is larger.
- ``Fact''
- indicates whether we need extra matrix storage.
``
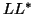 '' means a sparse Cholesky factorization, ``
'' means a sparse Cholesky factorization, ``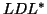 ,'' a
sparse symmetric indefinite Gaussian elimination, and ``ILU'' is an
incomplete factorization. It is supposed to be more compact and need less
arithmetic work than the other two.
,'' a
sparse symmetric indefinite Gaussian elimination, and ``ILU'' is an
incomplete factorization. It is supposed to be more compact and need less
arithmetic work than the other two.
We note that a task such as counting the
number of eigenvalues of 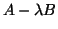 that are smaller than a given real
number
that are smaller than a given real
number 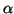 or are in a given interval
or are in a given interval
![$[\alpha, \beta]$](img202.png) does not require computing the eigenvalues, and so can be much cheaper.
The key tool is the matrix inertia as presented in
§4.1 (p.
does not require computing the eigenvalues, and so can be much cheaper.
The key tool is the matrix inertia as presented in
§4.1 (p. ![[*]](http://www.netlib.org/utk/icons/crossref.png) ).
It can be extended easily to the case of
).
It can be extended easily to the case of 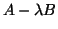 assuming
assuming
 positive definite. In summary, let
positive definite. In summary, let
be the LDL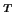 factorizations of matrices
factorizations of matrices
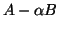 and
and 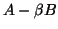 , respectively,
where we assume that
, respectively,
where we assume that
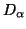 and
and 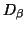 are nonsingular diagonal matrices.
We refer to
§10.3 for the information on software availability for
the LDL
are nonsingular diagonal matrices.
We refer to
§10.3 for the information on software availability for
the LDL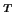 factorization.
Then the number of eigenvalues of
factorization.
Then the number of eigenvalues of 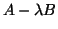 in
in
![$[\alpha, \beta]$](img202.png) equals
equals
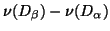 ,
where
,
where 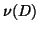 denotes the number of negative diagonal elements.
denotes the number of negative diagonal elements.





Next: Transformation to Standard Problem
Up: Introduction
Previous: Eigenvalues Sought.
Contents
Index
Susan Blackford
2000-11-20
![]() that are smaller than a given real
number
that are smaller than a given real
number ![]() or are in a given interval
or are in a given interval
![]() does not require computing the eigenvalues, and so can be much cheaper.
The key tool is the matrix inertia as presented in
§4.1 (p.
does not require computing the eigenvalues, and so can be much cheaper.
The key tool is the matrix inertia as presented in
§4.1 (p. ![]() ).
It can be extended easily to the case of
).
It can be extended easily to the case of ![]() assuming
assuming
![]() positive definite. In summary, let
positive definite. In summary, let