




Next: Overview of Available Algorithms.
Up: Hermitian Eigenvalue Problems
Previous: Hermitian Eigenvalue Problems
Contents
Index
Introduction
In this chapter we treat the standard Hermitian, or most often real
symmetric, eigenvalue problem (HEP),
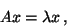 |
(16) |
where 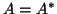 .
It is the most commonly occurring algebraic eigenvalue problem, for which
we have the most reliable theory and the most powerful algorithms available.
.
It is the most commonly occurring algebraic eigenvalue problem, for which
we have the most reliable theory and the most powerful algorithms available.
A summary of the basic theory about
the Hermitian eigenvalue problem (4.1)
is given in §2.2.
It is known that the problem (4.1) has  real eigenvalues
real eigenvalues
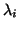 , which we may order increasingly so that
, which we may order increasingly so that
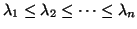 . Note that several
eigenvalues may coincide. In many applications the matrix
. Note that several
eigenvalues may coincide. In many applications the matrix  is
positive definite,
is
positive definite, 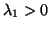 (or positive semidefinite,
(or positive semidefinite,
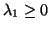 ).
Even in the cases
where positive definiteness can be used to advantage,
we choose to treat Hermitian
).
Even in the cases
where positive definiteness can be used to advantage,
we choose to treat Hermitian  with a general
distribution of eigenvalues in this chapter.
with a general
distribution of eigenvalues in this chapter.
When  is Hermitian, it is always possible to find
is Hermitian, it is always possible to find  mutually
orthogonal eigenvectors,
mutually
orthogonal eigenvectors,
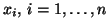 , so that
, so that
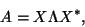 |
(17) |
where
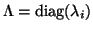 ,
,
![$X=[x_1,x_2,\dots,x_n]$](img758.png) , and
, and
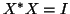 . The eigenvectors
. The eigenvectors 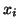 are not unique; what is unique is the
invariant subspace for each different eigenvalue.
For a Hermitian matrix
are not unique; what is unique is the
invariant subspace for each different eigenvalue.
For a Hermitian matrix  , the invariant subspace is of the same dimension
as the multiplicity of the eigenvalue. It is important to keep in mind that
when certain eigenvalues coincide, their eigenvectors lose
their individuality: there is no way of saying that one set of vectors
are the eigenvectors of a multiple eigenvalue.
Two different algorithms, and even two different runs with the same algorithm,
will give different representative eigenvectors in the invariant subspace.
On the other hand, a user is entitled to demand that an algorithm produce
eigenvector approximations that are orthogonal to each other,
even if the matrix has multiple eigenvalues.
, the invariant subspace is of the same dimension
as the multiplicity of the eigenvalue. It is important to keep in mind that
when certain eigenvalues coincide, their eigenvectors lose
their individuality: there is no way of saying that one set of vectors
are the eigenvectors of a multiple eigenvalue.
Two different algorithms, and even two different runs with the same algorithm,
will give different representative eigenvectors in the invariant subspace.
On the other hand, a user is entitled to demand that an algorithm produce
eigenvector approximations that are orthogonal to each other,
even if the matrix has multiple eigenvalues.
The eigenvalues of  are always well-conditioned.
If a perturbation
are always well-conditioned.
If a perturbation 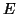 is added to the matrix
is added to the matrix  ,
then each of the eigenvalues is perturbed at most as far as
the spectral norm
,
then each of the eigenvalues is perturbed at most as far as
the spectral norm 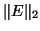 ,
,
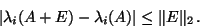 |
(18) |
There are several stronger results available, like the
Wielandt-Hoffman inequality that says that the sum of squares
of the differences between the eigenvalues is majorized
by the sum of squares of the elements of 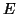 ; see §4.8 and
references therein.
In many cases, one is interested in eigenvalues that are small compared
to the norm
; see §4.8 and
references therein.
In many cases, one is interested in eigenvalues that are small compared
to the norm 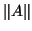 , and for such eigenvalues the inequality (4.3)
is not very satisfactory, since it allows large
relative perturbations for such small eigenvalues. It is possible
to develop perturbation bounds for relative perturbations under certain
additional assumptions.
, and for such eigenvalues the inequality (4.3)
is not very satisfactory, since it allows large
relative perturbations for such small eigenvalues. It is possible
to develop perturbation bounds for relative perturbations under certain
additional assumptions.
There is no result as simple as (4.3) available for
bounding the perturbation of eigenvectors: one has to add an
assumption of separation between the eigenvalues.
Let us cite the
venerable  theorem of Davis and Kahan from [101].
theorem of Davis and Kahan from [101].
Let us assume that  is
an approximation of the eigenpair
is
an approximation of the eigenpair
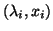 of
of  ,
where
,
where 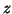 is normalized so that
is normalized so that 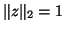 .
The ``best''
.
The ``best'' 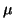 corresponding to
corresponding to 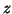 is the Rayleigh quotient
is the Rayleigh quotient
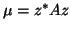 ,
so we assume that
,
so we assume that 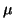 has this value.
Suppose that
has this value.
Suppose that 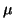 is closer
to
is closer
to 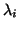 than any other eigenvalues of
than any other eigenvalues of  , and
let
, and
let 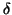 be the gap between
be the gap between
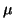 and any other eigenvalue:
and any other eigenvalue:
 .
Define the residual vector
.
Define the residual vector 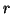 as
as 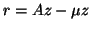 ; then we have
; then we have
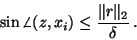 |
(19) |
Under the same assumptions, we have the improved bound on the eigenvalue
approximation,
|-_i|{||r||_2,||r||_2^2}.
The first alternative in this minimum is equivalent to the previous
bound (4.3), since 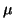 is an eigenvalue of the perturbed
matrix
is an eigenvalue of the perturbed
matrix 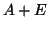 with
with  a rank-one perturbation of
norm
a rank-one perturbation of
norm
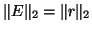 (it is not necessary for
(it is not necessary for 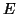 to be
Hermitian in the bound (4.3)).
The reader is referred to §4.8 for further details.
to be
Hermitian in the bound (4.3)).
The reader is referred to §4.8 for further details.
Subsections





Next: Overview of Available Algorithms.
Up: Hermitian Eigenvalue Problems
Previous: Hermitian Eigenvalue Problems
Contents
Index
Susan Blackford
2000-11-20
![]() real eigenvalues
real eigenvalues
![]() , which we may order increasingly so that
, which we may order increasingly so that
![]() . Note that several
eigenvalues may coincide. In many applications the matrix
. Note that several
eigenvalues may coincide. In many applications the matrix ![]() is
positive definite,
is
positive definite, ![]() (or positive semidefinite,
(or positive semidefinite,
![]() ).
Even in the cases
where positive definiteness can be used to advantage,
we choose to treat Hermitian
).
Even in the cases
where positive definiteness can be used to advantage,
we choose to treat Hermitian ![]() with a general
distribution of eigenvalues in this chapter.
with a general
distribution of eigenvalues in this chapter.
![]() is Hermitian, it is always possible to find
is Hermitian, it is always possible to find ![]() mutually
orthogonal eigenvectors,
mutually
orthogonal eigenvectors,
![]() , so that
, so that
![]() are always well-conditioned.
If a perturbation
are always well-conditioned.
If a perturbation ![]() is added to the matrix
is added to the matrix ![]() ,
then each of the eigenvalues is perturbed at most as far as
the spectral norm
,
then each of the eigenvalues is perturbed at most as far as
the spectral norm ![]() ,
,
![]() theorem of Davis and Kahan from [101].
theorem of Davis and Kahan from [101].
![]() is
an approximation of the eigenpair
is
an approximation of the eigenpair
![]() of
of ![]() ,
where
,
where ![]() is normalized so that
is normalized so that ![]() .
The ``best''
.
The ``best'' ![]() corresponding to
corresponding to ![]() is the Rayleigh quotient
is the Rayleigh quotient
![]() ,
so we assume that
,
so we assume that ![]() has this value.
Suppose that
has this value.
Suppose that ![]() is closer
to
is closer
to ![]() than any other eigenvalues of
than any other eigenvalues of ![]() , and
let
, and
let ![]() be the gap between
be the gap between
![]() and any other eigenvalue:
and any other eigenvalue:
![]() .
Define the residual vector
.
Define the residual vector ![]() as
as ![]() ; then we have
; then we have