Matrix Preparation.

For each algorithm we have distinguished between different ways of preparing the matrix prior to running the algorithm.

``Dir''

is direct application, where we perform a matrix multiply on a vector in each step. It is the simplest variant to apply, since the matrix can be stored in any compact way. On the other hand, most algorithms need many matrix-vector multiplications to converge and are restricted to seeking eigenvalues at the ends of the spectrum.

``SI''

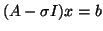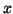is the shift-and-invert which needs a factorization routine to enable solutions of systems $(A-\sigma I)x=b$ for $x$, but gives the ability to compute a wider choice of eigenvalues in fewer iterations.

``Prec''

means application with a preconditioner, for instance, a sparse approximate factorization. This requires less space than the shift-and-invert, but most often it also needs a larger number of matrix-vector multiplies.