Results for L-Shaped Membrane.

The extremal eigenvalues are the first to converge for a direct application of a Lanczos algorithm, and in this case the convergence will be very similar in either end of the spectrum.

Figure 4.1: Residual estimates, L-shaped membrane matrix.

Figure 4.2: Ritz values, L-shaped membrane matrix.

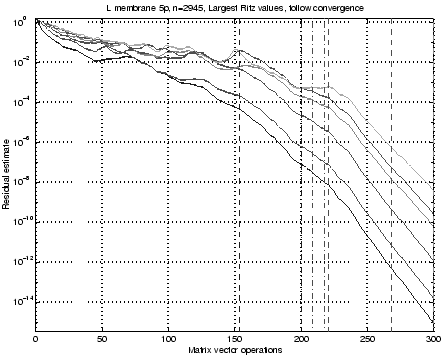
We have plotted the estimated residuals (4.13) for the six largest eigenvalues as a function of the number $j$ of Lanczos steps in Figure 4.1. The curves show the residual estimates (4.13) for each step and were computed only for illustration purposes after the actual computation. The LANSO algorithm called the QL algorithm to compute eigenvalues and last elements of eigenvectors to test for convergence (4.13), at the iterations marked with dashdotted vertical lines in the plot. The selective orthogonalization triggered reorthogonalization at the steps we marked with dashed lines, altogether only three times during all these $300$ steps. This is typical for situations with a slow convergence: orthogonality is preserved until the first Ritz value converges.

Note that a relatively large number of steps, about $150$, are needed to bring the residual of the leading eigenvalue down to $10^{-4}$, and that another $150$ steps are taken before full machine accuracy is reached. Looking at the Ritz values $\theta^{(j)}_i$ of (4.11) plotted versus $j$ in Figure 4.2, we see that the largest Ritz value grows with $j$ until around step $j=60$, when it stabilizes. Frequently a Ritz value will start to approach one eigenvalue, but will later move to another, not yet found, eigenvalue. This happens with the third Ritz value at steps $60$ to $80$ and becomes more pronounced with the sixth between steps $150$ and $210$. This phenomenon shows up in a less evident fashion in Figure 4.1, where the third and sixth curves from the bottom have plateaus at the steps when a Ritz value shifts allegiance. A user of a direct Lanczos method is advised to take care when deciding whether all the largest eigenvalues really have converged.

Figure 4.3: Residual estimates, Medline SVD matrix

Figure 4.4: Residual estimates, shift-and-invert L-shaped membrane matrix.