




Next: Results for L-Shaped Membrane
Up: Numerical Examples
Previous: Results for L-Shaped Membrane.
Contents
Index
The second test example, Medline SVD, behaves quite differently. The
leading eigenvalues (
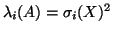 ) are quite well
separated (the largest one is
) are quite well
separated (the largest one is
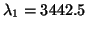 and the next one is
and the next one is
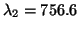 ), and even if the quotients
), and even if the quotients
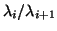 are smaller for larger
are smaller for larger 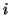 , we will get fast convergence as
indicated in Figure 4.3. The first eigenvalue reaches full
accuracy already at step
, we will get fast convergence as
indicated in Figure 4.3. The first eigenvalue reaches full
accuracy already at step 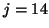 , and after
, and after 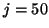 steps the first 6
eigenvalues are converged. After
steps the first 6
eigenvalues are converged. After 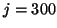 steps we had 100 eigenvalues.
steps we had 100 eigenvalues.
There is another interesting difference between this well-separated
problem and the L-shaped membrane with its more clustered eigenvalues in that
reorthogonalization is triggered more often. We mark reorthogonalizations
with a dashed vertical line at step 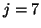 , one at
, one at 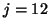 , and
every four steps from there on. Since each reorthogonalization involves two vectors,
selective reorthogonalization demands about half as much work as a
full reorthogonalization. In such cases the user is advised
to use full reorthogonalization, since it gives full orthogonality of the
basis vectors at a moderate extra cost in arithmetic work.
, and
every four steps from there on. Since each reorthogonalization involves two vectors,
selective reorthogonalization demands about half as much work as a
full reorthogonalization. In such cases the user is advised
to use full reorthogonalization, since it gives full orthogonality of the
basis vectors at a moderate extra cost in arithmetic work.





Next: Results for L-Shaped Membrane
Up: Numerical Examples
Previous: Results for L-Shaped Membrane.
Contents
Index
Susan Blackford
2000-11-20
![]() , one at
, one at ![]() , and
every four steps from there on. Since each reorthogonalization involves two vectors,
selective reorthogonalization demands about half as much work as a
full reorthogonalization. In such cases the user is advised
to use full reorthogonalization, since it gives full orthogonality of the
basis vectors at a moderate extra cost in arithmetic work.
, and
every four steps from there on. Since each reorthogonalization involves two vectors,
selective reorthogonalization demands about half as much work as a
full reorthogonalization. In such cases the user is advised
to use full reorthogonalization, since it gives full orthogonality of the
basis vectors at a moderate extra cost in arithmetic work.