




Next: Reorthogonalization
Up: Lanczos Method A.
Previous: Multiple Eigenvalues.
Contents
Index
Spectral Transformation
If the extreme eigenvalues are not well separated and when we want interior
eigenvalues,
it is greatly advantageous to replace
 by a shift-and-invert operator
by a shift-and-invert operator
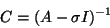 |
(28) |
for an appropriately chosen shift 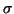 , for instance, in the interval
, for instance, in the interval
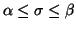 , where we are interested in knowing the
eigenvalues. The shift-and-invert operator
, where we are interested in knowing the
eigenvalues. The shift-and-invert operator 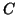 has
the eigenvalues
has
the eigenvalues
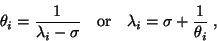 |
(29) |
and now the eigenvalues 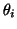 that correspond to eigenvalues
that correspond to eigenvalues
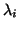 close to the shift
close to the shift 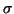 will be at the ends of the
spectrum and well separated from the rest; see [162].
will be at the ends of the
spectrum and well separated from the rest; see [162].
If we use a shift-and-invert operator, we start the algorithm by factoring
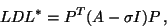 |
(30) |
using some appropriate sparse Gaussian
elimination scheme. Here, 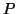 is a permutation and
is a permutation and 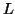 is unit lower triangular.
If there are eigenvalues
is unit lower triangular.
If there are eigenvalues  at both sides
of the shift
at both sides
of the shift 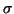 , we cannot use
a scalar diagonal
, we cannot use
a scalar diagonal 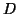 , but we have to make a symmetric
indefinite factorization, as in MA47 of Duff and Reid
[141]. Here
, but we have to make a symmetric
indefinite factorization, as in MA47 of Duff and Reid
[141]. Here 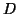 is block diagonal with one by one
and two by two blocks, and we get the inertia of
is block diagonal with one by one
and two by two blocks, and we get the inertia of 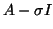 as a by-product. We can get a count of the number of
eigenvalues in an interval by recording the inertia of
as a by-product. We can get a count of the number of
eigenvalues in an interval by recording the inertia of 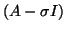 for two values
for two values 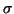 at the ends of the interval. Obtaining this count is used
to make sure that no multiple eigenvalues are missed.
See §10.3 for further information about
sparse matrix factorizations.
at the ends of the interval. Obtaining this count is used
to make sure that no multiple eigenvalues are missed.
See §10.3 for further information about
sparse matrix factorizations.
During the actual iteration, we use the factors 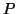 ,
, 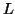 , and
, and 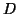 , computing
, computing
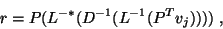 |
(31) |
in the order indicated by the parentheses,
in step (5) of Algorithm 4.6.





Next: Reorthogonalization
Up: Lanczos Method A.
Previous: Multiple Eigenvalues.
Contents
Index
Susan Blackford
2000-11-20
![]() by a shift-and-invert operator
by a shift-and-invert operator
![]() ,
, ![]() , and
, and ![]() , computing
, computing