




Next: Full Reorthogonalization.
Up: Lanczos Method A.
Previous: Spectral Transformation
Contents
Index
Reorthogonalization
The Lanczos recursion is constructed to make the basis 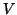 orthogonal,
but this is true only for infinite precision computation. In the
algorithm we only make sure that the new vector
orthogonal,
but this is true only for infinite precision computation. In the
algorithm we only make sure that the new vector 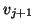 is
orthogonal to working
precision to the two latest vectors
is
orthogonal to working
precision to the two latest vectors 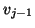 and
and 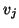 ,
and orthogonality to the earlier vectors follows from the symmetry of
,
and orthogonality to the earlier vectors follows from the symmetry of
 and the recursion (4.10). As soon as one
eigenvalue converges, i.e., the Ritz pair has a small residual (
and the recursion (4.10). As soon as one
eigenvalue converges, i.e., the Ritz pair has a small residual (![[*]](http://www.netlib.org/utk/icons/crossref.png) ), all the basis vectors
), all the basis vectors 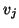 get perturbations in the
direction of the eigenspace of the converged eigenvalue. As a result of this,
a duplicate copy of that eigenvalue will soon show up in
the tridiagonal matrix
get perturbations in the
direction of the eigenspace of the converged eigenvalue. As a result of this,
a duplicate copy of that eigenvalue will soon show up in
the tridiagonal matrix 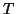 .
Paige [347] was the first to discover this; the reader is
referred to the monograph [353] for a detailed discussion.
.
Paige [347] was the first to discover this; the reader is
referred to the monograph [353] for a detailed discussion.
Let us consider three different strategies to handle this.
Subsections
Susan Blackford
2000-11-20