




Next: List of Tables
Up: book
Previous: List of Direct Algorithms
Contents
Index
- Damped, vibrating mass-spring system.
- Residual estimates, L-shaped membrane matrix.
- Ritz values, L-shaped membrane matrix.
- Residual estimates, Medline SVD matrix
- Residual estimates, shift-and-invert L-shaped membrane matrix.
- Jacobi-Davidson for exterior eigenvalues with several
strategies for solving the correction equation.
- Jacobi-Davidson for exterior eigenvalues (top)
and interior eigenvalues (bottom). The correction equations have been
solved with 5 steps of plain GMRES (left)
and with 5 steps of preconditioned GMRES (right).
- Residual estimates, Lanczos with shift-and-invert,
L-membrane 9-point finite difference approximation.
- Relative
accuracy of eigenvalues computed with and without direct balancing
for the QH
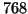 and TOLOSA matrices.
and TOLOSA matrices.
- Relative accuracy
of eigenvalues computed with and without Krylov balancing for the
QH
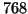 and TOLOSA matrices.
and TOLOSA matrices.
- Comparison of the relative
accuracy of the largest and smallest (in magnitude) eigenvalues of
the QH
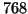 matrix, with different Krylov-based balancing algorithms,
using the default settings of five iterations and a cutoff value of
matrix, with different Krylov-based balancing algorithms,
using the default settings of five iterations and a cutoff value of
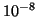 .
.
- Comparison of the relative
accuracy of the largest and smallest (in magnitude) eigenvalues of
the TOLOSA matrix, with different Krylov-based balancing algorithms,
using the default settings of five iterations and a cutoff value of
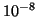 .
.
- Jacobi-Davidson for exterior eigenvalues (left side)
and interior eigenvalues (right side).
- Convergence history for BFW
 .
.
- Procrustes problem
- Jordan problem
- Trace minimization problem
- LDA toy problem
- Simultaneous Schur problem
- Simultaneous diagonalization problem
- The unconstrained differential of
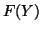 can be projected
to the tangent space to obtain the covariant gradient,
can be projected
to the tangent space to obtain the covariant gradient, 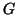 , of
, of 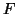 .
.
- In a flat space, comparing vectors at nearby
points is not problematic since all vectors lie in the same
tangent space.
- In a curved manifold, comparing vectors at nearby
points can result in vectors which do not lie in the tangent space.
- Profile of a nonsymmetric skyline or variable-band
matrix.
- Logarithmic plots of residual norms of the inexact rational
Krylov
method for the Olmstead problem. The circles denote
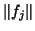 and the
bullets
and the
bullets 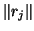 .
.
- Conjugate gradient versus steepest ascent,
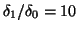
- Conjugate gradient versus steepest ascent,
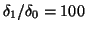
- Conjugate gradient versus steepest ascent,
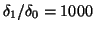
Susan Blackford
2000-11-20