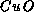Following the discovery of high-temperature
superconductivity, two-dimensional quantum
antiferromagnetic spin systems have received enormous attention from
physicists worldwide. It is generally believed that high-temperature
superconductivity occurs in the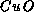 
planes, which is shown in
Figure 6.4. Many features can be explained [Anderson:87a] in
the Hubbard theory of the strongly coupled electron, which at half-filling is
reduced to spin-1/2 antiferromagnetic Heisenberg
model:
where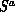 
are quantum spin operators. Furthermore, the
neutron scattering experiments on the parent compound,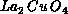 
,
reveal a rich magnetic structure which is also modelled by this theory.
Physics in two dimensions (as compared to three dimensions) is characterized by the large fluctuations. Many analytical methods work well in three dimensions, but fail in two dimensions. For the quantum systems, this means additional difficulties in finding solutions to the problem.
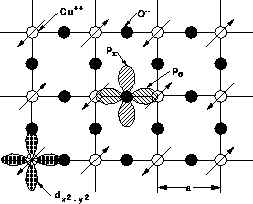
Figure 6.4: The Copper-Oxygen Plane, Where the Superconductivity Is
Generally Believed to Occur. The arrows denote the quantum spins.
, 
, 
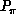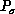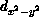denote the wave functions which
lead to the interactions among them.
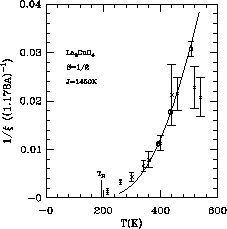
Figure: Inverse Correlation Length of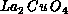 
Measured in Neutron
Scattering Experiment, Denoted by Cross; and Those Measured in our
Simulation, Denoted by Squares (Units in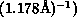 
.
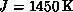. At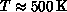 
, 
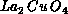undergoes a structural transition. The curve is the fit shown in
Figure 6.11.
New analytical methods have been developed to understand the low-T behavior
of these two-dimensional systems, and progress had been made. These methods
are essentially based on a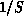 
expansion. Unfortunately, the extreme
quantum case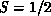 
lies in the least reliable region of these
methods. On the other hand, given sufficient computer power, Quantum Monte
Carlo simulation [Ding:90g] can provide
accurate numerical solutions of the model theory and quantitative comparison
with the experiment (see Figure 6.5). Thus, simulations become a
crucial tool in studying these problems. The work described here has made a
significant contribution to the understanding of high-
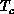materials, and
has been well received by the science community [Maddox:90a].
