




Next: 4.3.5 Concurrent QCD Machines
Up: 4.3 Quantum Chromodynamics
Previous: 4.3.3 QCD
To put QCD on a computer, we proceed as follows [Wilson:74a],
[Creutz:83a]. The four-dimensional
space-time continuum is replaced by a four-dimensional hypercubic periodic
lattice of size 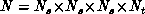 , with the
quarks living on the sites and the gluons living on the links of the lattice.
, with the
quarks living on the sites and the gluons living on the links of the lattice.
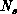 is the spatial and
is the spatial and  is the temporal extent of the lattice. The
lattice has a finite spacing a. The gluons are represented by
is the temporal extent of the lattice. The
lattice has a finite spacing a. The gluons are represented by
 complex SU(3) matrices associated with each link in the
lattice. The 3 in SU(3) reflects the fact that there are three colors of
quarks, and SU means that the matrices are unitary with unit determinant
(i.e., ``special unitary''). This link matrix describes how the color
of a quark changes as it moves from one site to the next. For example, as a
quark is transported along a link of the lattice it can change its color
from, say, red to green; hence, a red quark at one end of the link can
exchange colors with a green quark at the other end. The action functional
for the purely gluonic part of QCD is
complex SU(3) matrices associated with each link in the
lattice. The 3 in SU(3) reflects the fact that there are three colors of
quarks, and SU means that the matrices are unitary with unit determinant
(i.e., ``special unitary''). This link matrix describes how the color
of a quark changes as it moves from one site to the next. For example, as a
quark is transported along a link of the lattice it can change its color
from, say, red to green; hence, a red quark at one end of the link can
exchange colors with a green quark at the other end. The action functional
for the purely gluonic part of QCD is

where 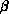 is a coupling constant and
is a coupling constant and

is the product of link matrices around an elementary square or plaquette on
the lattice-see Figure 4.8. Essentially all of the time in
QCD simulations of gluons is spent multiplying these SU(3) matrices
together. The main component of this is the  kernel, which
most supercomputers can do very efficiently. As the action involves
interactions around plaquettes, in order to satisfy detailed
balance we can update only half the links in any one
dimension simultaneously, as shown in Figure 4.9 (in two dimensions
for simplicity). The partition function for full-lattice QCD including quarks
is
kernel, which
most supercomputers can do very efficiently. As the action involves
interactions around plaquettes, in order to satisfy detailed
balance we can update only half the links in any one
dimension simultaneously, as shown in Figure 4.9 (in two dimensions
for simplicity). The partition function for full-lattice QCD including quarks
is

where 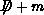 is a large sparse matrix the
size of the lattice squared. Unfortunately, since the quark or fermion
variables
is a large sparse matrix the
size of the lattice squared. Unfortunately, since the quark or fermion
variables 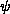 are anticommuting Grassmann numbers, there is no
simple representation for them on the computer. Instead, they must be
integrated out, leaving a highly non-local fermion determinant:
are anticommuting Grassmann numbers, there is no
simple representation for them on the computer. Instead, they must be
integrated out, leaving a highly non-local fermion determinant:
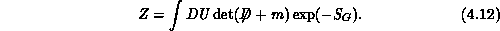
This is the basic integral one wants to evaluate numerically.

Figure 4.8: A Lattice Plaquette

Figure 4.9: Updating the Lattice
The biggest stumbling block preventing large QCD simulations with
quarks is the presence of the determinant  in the
partition function. There have been many proposals for dealing with the
determinant. The first algorithms tried to compute the change in the
determinant when a single link variable was updated [Weingarten:81a].
This turned out to be prohibitively expensive. So instead, the approximate
method of pseudo-fermions [Fucito:81a] was used.
Today, however, the preferred approach is the so-called Hybrid Monte
Carlo algorithm [Duane:87a], which is exact.
The basic idea is to invent some dynamics for the variables in the system in
order to evolve the whole system forward in (simulation) time, and then do a
Metropolis accept/reject for the entire evolution on the basis of the total
energy change. The great advantage is that the whole system is updated in
one fell swoop. The disadvantage is that if the dynamics are not correct,
the acceptance will be very small. Fortunately (and this is one of very few
fortuitous happenings where fermions are concerned), good dynamics can be
found: the Hybrid algorithm [Duane:85a]. This is a neat combination
of the deterministic microcanonical method [Callaway:83a],
[Polonyi:83a] and the stochastic Langevin method [Parisi:81a],
[Batrouni:85a], which yields a quickly evolving, ergodic algorithm for
both gauge fields and fermions. The computational kernel of this algorithm
is the repeated solution of systems of equations of the form
in the
partition function. There have been many proposals for dealing with the
determinant. The first algorithms tried to compute the change in the
determinant when a single link variable was updated [Weingarten:81a].
This turned out to be prohibitively expensive. So instead, the approximate
method of pseudo-fermions [Fucito:81a] was used.
Today, however, the preferred approach is the so-called Hybrid Monte
Carlo algorithm [Duane:87a], which is exact.
The basic idea is to invent some dynamics for the variables in the system in
order to evolve the whole system forward in (simulation) time, and then do a
Metropolis accept/reject for the entire evolution on the basis of the total
energy change. The great advantage is that the whole system is updated in
one fell swoop. The disadvantage is that if the dynamics are not correct,
the acceptance will be very small. Fortunately (and this is one of very few
fortuitous happenings where fermions are concerned), good dynamics can be
found: the Hybrid algorithm [Duane:85a]. This is a neat combination
of the deterministic microcanonical method [Callaway:83a],
[Polonyi:83a] and the stochastic Langevin method [Parisi:81a],
[Batrouni:85a], which yields a quickly evolving, ergodic algorithm for
both gauge fields and fermions. The computational kernel of this algorithm
is the repeated solution of systems of equations of the form
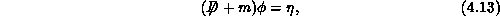
where 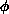 and
and 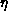 are vectors that live on the sites of the
lattice. To solve these equations, one typically uses a conjugate
gradient algorithm or one of its cousins,
since the fermion matrix
are vectors that live on the sites of the
lattice. To solve these equations, one typically uses a conjugate
gradient algorithm or one of its cousins,
since the fermion matrix 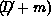 is sparse. For more
details, see [Gupta:88a]. Such iterative matrix algorithms have
as their basic component the
is sparse. For more
details, see [Gupta:88a]. Such iterative matrix algorithms have
as their basic component the  kernel, so again
computers which do this efficiently will run QCD well.
kernel, so again
computers which do this efficiently will run QCD well.





Next: 4.3.5 Concurrent QCD Machines
Up: 4.3 Quantum Chromodynamics
Previous: 4.3.3 QCD
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
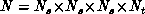 , with the
quarks living on the sites and the gluons living on the links of the lattice.
, with the
quarks living on the sites and the gluons living on the links of the lattice.
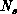 is the spatial and
is the spatial and  is the temporal extent of the lattice. The
lattice has a finite spacing a. The gluons are represented by
is the temporal extent of the lattice. The
lattice has a finite spacing a. The gluons are represented by
 complex SU(3) matrices associated with each link in the
lattice. The 3 in SU(3) reflects the fact that there are three colors of
quarks, and SU means that the matrices are unitary with unit determinant
(i.e., ``special unitary''). This link matrix describes how the color
of a quark changes as it moves from one site to the next. For example, as a
quark is transported along a link of the lattice it can change its color
from, say, red to green; hence, a red quark at one end of the link can
exchange colors with a green quark at the other end. The action functional
for the purely gluonic part of QCD is
complex SU(3) matrices associated with each link in the
lattice. The 3 in SU(3) reflects the fact that there are three colors of
quarks, and SU means that the matrices are unitary with unit determinant
(i.e., ``special unitary''). This link matrix describes how the color
of a quark changes as it moves from one site to the next. For example, as a
quark is transported along a link of the lattice it can change its color
from, say, red to green; hence, a red quark at one end of the link can
exchange colors with a green quark at the other end. The action functional
for the purely gluonic part of QCD is






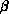 is a coupling constant and
is a coupling constant and

 kernel, which
most supercomputers can do very efficiently. As the action involves
interactions around plaquettes, in order to satisfy detailed
balance
kernel, which
most supercomputers can do very efficiently. As the action involves
interactions around plaquettes, in order to satisfy detailed
balance
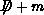 is a large sparse matrix
is a large sparse matrix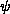 are anticommuting Grassmann numbers, there is no
simple representation for them on the computer. Instead, they must be
integrated out, leaving a highly non-local fermion determinant:
are anticommuting Grassmann numbers, there is no
simple representation for them on the computer. Instead, they must be
integrated out, leaving a highly non-local fermion determinant:
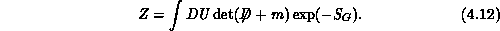


 in the
partition function. There have been many proposals for dealing with the
determinant. The first algorithms tried to compute the change in the
determinant when a single link variable was updated [
in the
partition function. There have been many proposals for dealing with the
determinant. The first algorithms tried to compute the change in the
determinant when a single link variable was updated [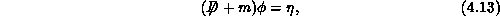
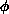 and
and 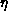 are vectors that live on the sites of the
lattice. To solve these equations, one typically uses a conjugate
gradient
are vectors that live on the sites of the
lattice. To solve these equations, one typically uses a conjugate
gradient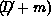 is sparse. For more
details, see [
is sparse. For more
details, see [ kernel, so again
computers which do this efficiently will run QCD well.
kernel, so again
computers which do this efficiently will run QCD well.