QCD describes the interactions between quarks in high energy physics. Currently, we know of five types (referred to as ``flavors'') of quark: up, down, strange, charm, and bottom; and expect one more (top) to show up soon. In addition to having a ``flavor,'' quarks can carry one of three possible charges known as ``color'' (this has nothing to do with color in the macroscopic world!); hence, quantum chromodynamics. The strong color force is mediated by particles called gluons, just as photons mediate the electromagnetic force. Unlike photons, though, gluons themselves carry a color charge and, therefore, interact with one another. This makes QCD a nonlinear theory, which is impossible to solve analytically. Therefore, we turn to the computer for numerical solutions.
QCD is an example of a ``gauge theory.'' These are quantum field
theories that have a local symmetry described by a symmetry (or gauge)
group. Gauge theories are ubiquitous in
elementary particle physics: The electromagnetic interaction
between electrons and photons is described by quantum electrodynamics
(QED) based on the gauge group U(1); the strong force between quarks
and gluons is believed to be explained by QCD based on the group
SU(3); and there is a unified description of the weak and
electromagnetic interactions in terms of the
gauge group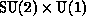 
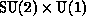. The strength of these interactions
is measured by a coupling constant. This coupling constant is small
for QED, so very precise analytical calculations can be performed using
perturbation theory, and these agree extremely well with experiment.
However, for QCD, the coupling appears to increase with distance (which
is why we never see an isolated quark, since they are always bound
together by the strength of the coupling between them). Perturbative
calculations are therefore only possible at short distances (or large
energies). In order to solve QCD at longer distances, Wilson
[Wilson:74a] introduced lattice gauge theory,
in which the space-time continuum is discretized and a discrete version
of the gauge theory is derived which keeps the gauge symmetry intact.
This discretization onto a lattice, which is typically hypercubic,
gives a nonperturbative approximation to the theory that is
successively improvable by increasing the lattice size and decreasing
the lattice spacing, and provides a simple and natural way of
regulating the divergences which plague perturbative approximations.
It also makes the gauge theory amenable to numerical simulation by
computer.