




Next: Exploitation of Latency
Up: Single Integration Step
Previous: Single Residuals
There is evidently much more available
concurrency in this computational step than for the single residual and
integration operations, since, for finite differencing, N independent
residual computations are apparently required, each of which is a
single-state perturbation of 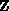 . Based on our overview of the
residual computation, we might naively expect to use
. Based on our overview of the
residual computation, we might naively expect to use 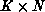 processes
effectively; however, the simple perturbations can actually require much
less model evaluation effort because of latency
[Duff:86a], [Kuru:81a], which is directly a function of the
sparsity structure of the model equations as seen in,
Equation 9.11. In short, we can attain the same
performance with much less than
processes
effectively; however, the simple perturbations can actually require much
less model evaluation effort because of latency
[Duff:86a], [Kuru:81a], which is directly a function of the
sparsity structure of the model equations as seen in,
Equation 9.11. In short, we can attain the same
performance with much less than 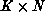 processors.
processors.
In general, we'd like to consider the Jacobian computation on a rectangular
grid. For this, we can consider using  to accomplish the
calculation. With a general grid shape, we exploit some concurrency in
both the column evaluations and the residual computations, with
to accomplish the
calculation. With a general grid shape, we exploit some concurrency in
both the column evaluations and the residual computations, with
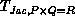 the time for this step,
the time for this step,
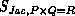 the corresponding speedup,
the corresponding speedup, 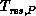 the
residual evaluation time with P row processes, and
the
residual evaluation time with P row processes, and 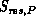 the
apparent speedup compared to one row process:
the
apparent speedup compared to one row process:

assuming no shortcuts are available as a result of latency. This timing is
exemplified in the example below, which does not take advantage of latency.
There is additional work whenever the Jacobian structure is rebuilt for
better numerical stability in the subsequent LU factorization (A-mode).
Then, 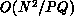 work is involved in each process in the filling of the
initial Jacobian. In the normal case, work proportional to the number of
local nonzeroes plus fill elements is incurred in each process for
refilling the sparse Jacobian structure.
work is involved in each process in the filling of the
initial Jacobian. In the normal case, work proportional to the number of
local nonzeroes plus fill elements is incurred in each process for
refilling the sparse Jacobian structure.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
 to accomplish the
calculation. With a general grid shape, we exploit some concurrency in
both the column evaluations and the residual computations, with
to accomplish the
calculation. With a general grid shape, we exploit some concurrency in
both the column evaluations and the residual computations, with
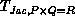 the time for this step,
the time for this step,
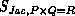 the corresponding speedup,
the corresponding speedup, 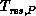 the
residual evaluation time with P row processes, and
the
residual evaluation time with P row processes, and 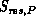 the
apparent speedup compared to one row process:
the
apparent speedup compared to one row process:





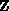 . Based on our overview of the
residual computation, we might naively expect to use
. Based on our overview of the
residual computation, we might naively expect to use 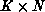 processes
effectively; however, the simple perturbations can actually require much
less model evaluation effort because of latency
[Duff:86a], [Kuru:81a], which is directly a function of the
sparsity structure of the model equations as seen in,
Equation 9.11. In short, we can attain the same
performance with much less than
processes
effectively; however, the simple perturbations can actually require much
less model evaluation effort because of latency
[Duff:86a], [Kuru:81a], which is directly a function of the
sparsity structure of the model equations as seen in,
Equation 9.11. In short, we can attain the same
performance with much less than 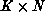 processors.
processors.

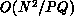 work is involved in each process in the filling of the
initial Jacobian. In the normal case, work proportional to the number of
local nonzeroes plus fill elements is incurred in each process for
refilling the sparse Jacobian structure.
work is involved in each process in the filling of the
initial Jacobian. In the normal case, work proportional to the number of
local nonzeroes plus fill elements is incurred in each process for
refilling the sparse Jacobian structure.