




Next: Jacobian Computation
Up: Single Integration Step
Previous: The Integration Computations
These are computed in prediction and as needed
during correction. Multiple residuals are computed when forming the
finite-difference Jacobian. Single residuals are computed repetitively in
each process column, whereas the multiple residuals of a Jacobian computation
are computed uniquely in the process columns.
Here, we consider the single residual computation required by the integration
computations just described. Given a state vector 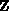 , and
approximation for
, and
approximation for  , we need to evaluate
, we need to evaluate
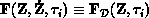 . The exploitable concurrency available in this step is strictly
a function of the model equations. As defined, there are N equations in
this system, so we expect to use at best N computers for this step.
Practically, there will be interprocess communication between the process
rows, corresponding to the connectivity among the equations. This will place
an upper limit on
. The exploitable concurrency available in this step is strictly
a function of the model equations. As defined, there are N equations in
this system, so we expect to use at best N computers for this step.
Practically, there will be interprocess communication between the process
rows, corresponding to the connectivity among the equations. This will place
an upper limit on 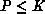 (the number of row processes) that can be used
before the speed will again decrease: We can expect efficient speedup for
this step provided that the cost of the interprocess communication is
insignificant compared to the single-equation grain size. As estimated in
[Skjellum:90a], the granularity
(the number of row processes) that can be used
before the speed will again decrease: We can expect efficient speedup for
this step provided that the cost of the interprocess communication is
insignificant compared to the single-equation grain size. As estimated in
[Skjellum:90a], the granularity 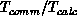 for the
Symult s2010 multicomputer is about fifty, so this implies about 450
floating-point operations per communication in order to achieve
90% concurrent efficiency in this phase.
for the
Symult s2010 multicomputer is about fifty, so this implies about 450
floating-point operations per communication in order to achieve
90% concurrent efficiency in this phase.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
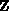 , and
approximation for
, and
approximation for  , we need to evaluate
, we need to evaluate
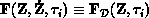 . The exploitable concurrency available in this step is strictly
a function of the model equations. As defined, there are N equations in
this system, so we expect to use at best N computers for this step.
Practically, there will be interprocess communication between the process
rows, corresponding to the connectivity among the equations. This will place
an upper limit on
. The exploitable concurrency available in this step is strictly
a function of the model equations. As defined, there are N equations in
this system, so we expect to use at best N computers for this step.
Practically, there will be interprocess communication between the process
rows, corresponding to the connectivity among the equations. This will place
an upper limit on 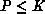 (the number of row processes) that can be used
before the speed will again decrease: We can expect efficient speedup for
this step provided that the cost of the interprocess communication is
insignificant compared to the single-equation grain size. As estimated in
[Skjellum:90a], the granularity
(the number of row processes) that can be used
before the speed will again decrease: We can expect efficient speedup for
this step provided that the cost of the interprocess communication is
insignificant compared to the single-equation grain size. As estimated in
[Skjellum:90a], the granularity 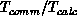 for the
Symult s2010 multicomputer is about fifty, so this implies about 450
floating-point operations per communication in order to achieve
90% concurrent efficiency in this phase.
for the
Symult s2010 multicomputer is about fifty, so this implies about 450
floating-point operations per communication in order to achieve
90% concurrent efficiency in this phase.




