We address the following initial-value problem consisting of combinations of
N linear and nonlinear coupled, ordinary differential-algebraic
equations over the interval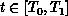 
:
IVP
:
with unknown state vector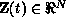 
, known external inputs
, where 
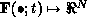and
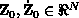are the given initial-value,
derivative vectors, respectively. We will refer to Equation 9.11's
deviation from 
as the residuals or residual vector. Evaluating the
residuals means computing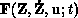 
(``model
evaluation'') for specified arguments 
, 
, 
and t.
DASSL's integration algorithm can be used to solve systems fully
implicit in 
and 
and of index zero or one, and
specially structured forms of index two (and higher)
[Brenan:89a, Chapter 5], where the index is the minimum number of times
that part or all of Equation 9.11 must be differentiated with
respect to t in order to express 
as a continuous function
of 
and t [Brenan:89a, page 17].
By substituting a finite-difference approximation 
for
, we obtain:
a set of (in general) nonlinear staticized equations. A sequence of
Equation 9.12's will have to be solved, one at each discrete time
, in the numerical
approximation scheme; neither M nor the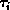 
's need be
predetermined. In DASSL, the variable step-size integration algorithm
picks the 
's as the integration progresses, based on its
assessment of the local error. The discretization operator for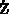 
, 
, varies during the numerical integration process and
hence is subscripted as 
.
The usual way to solve an instance of the staticized equations,
Equation 9.12, is via the familiar Newton-Raphson iterative
method (yielding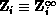 
):
given an initial, sufficiently good approximation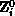 
. The
classical method is recovered for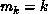 
and c = 1, whereas a modified
(damped) Newton-Raphson method results for 
(respectively,
). In the original DASSL algorithm and in Concurrent
DASSL, the Jacobian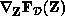 
is
computed by finite differences rather than
analytically; this departure leads in another sense to a modified
Newton-Raphson method even though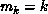 
and c = 1 might always
be satisfied. For termination, a limit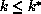 
is imposed; a
further stopping criterion of the form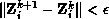 
is also incorporated (see Brenan et al.
[Brenan:89a, pages 121-124]).
Following Brenan et al., the approximation 
is
replaced by a BDF-generated linear approximation,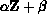 
,
and the Jacobian
From this approximation, we define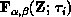 
in the intuitive way. We then consider Taylor's Theorem with
remainder, from which we can easily express a forward finite-difference
approximation for each Jacobian column (assuming sufficient smoothness of
) with a scaled difference of two residual vectors:
By picking 
proportional to 
, the
junit vector in the natural basis for 
, namely
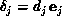, Equation 9.15 yields a
first-order-accurate approximation in 
of the jcolumn of the
Jacobian matrix:
Each of these N Jacobian-column computations is independent and trivially parallelizable. It's well known, however, that for special structures such as banded and block n-diagonal matrices, and even for general sparse matrices, a single residual can be used to generate multiple Jacobian columns [Brenan:89a], [Duff:86a]. We discuss these issues as part of the concurrent formulation section below.
The solution of the Jacobian linear system of equations is required for each
k-iteration, either through a direct (e.g., LU-factorization) or
iterative (e.g., preconditioned-conjugate-gradient) method. The most
advantageous solution approach depends on N as well as special mathematical
properties and/or structure of the Jacobian matrix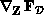 
. Together, the inner (linear equation solution) and
outer (Newton-Raphson iteration) loops solve a single
time point; the overall algorithm generates a sequence of solution points
.
In the present work, we restrict our attention to direct, sparse linear algebra as described in [Skjellum:90d], although future versions of Concurrent DASSL will support the iterative linear algebra approaches by Ashby, Lee, Brown, Hindmarsh et al. [Ashby:90a], [Brown:91a]. For the sparse LU factorization, the factors are stored and reused in the modified Newton scenario. Then, repeated use of the old Jacobian implies just a forward- and back-solve step using the triangular factors L and U. Practically, we can use the Jacobian for up to about five steps [Brenan:89a]. The useful lifetime of a single Jacobian evidently depends somewhat strongly on details of the integration procedure [Brenan:89a].
