




Next: 9.5.4 New Data Distributions
Up: LU Factorization of
Previous: 9.5.2 Design Overview
At each stage of the concurrent LU factorization, the pivot element is
chosen by the user-defined pivot function. Then, the pivot row (new
row of U) must be broadcast, and pivot column (new
column of L) must be computed and broadcast on the
logical process grid (cf., Figure 9.12), vertically
and horizontally, respectively. Note that these are interchangeable
operations. We use this degree of freedom to reduce the communication
complexity of particular pivoting strategies, while
impacting the effort of the LU factorization itself negligibly.
We define two ``correctness modes'' of pivoting functions. In the first
correctness mode, ``first row fanout,'' the exit conditions for the pivot
function are: All processes must know 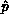 (the pivot process row); the
pivot process row must know
(the pivot process row); the
pivot process row must know 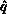 (the pivot process column) as well as
(the pivot process column) as well as
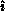 , the
, the 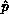 -local matrix row of the pivot; and the pivot
process must know in addition the pivot value and
-local matrix row of the pivot; and the pivot
process must know in addition the pivot value and 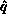 -local matrix
column
-local matrix
column 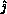 of the pivot. Partial column pivoting and preset
pivoting can be set up to satisfy these correctness conditions as follows. For
partial column pivoting, the krow is eliminated at the kstep of
the factorization. From this fact, each process can derive the process row
of the pivot. Partial column pivoting and preset
pivoting can be set up to satisfy these correctness conditions as follows. For
partial column pivoting, the krow is eliminated at the kstep of
the factorization. From this fact, each process can derive the process row
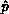 and
and  -local matrix row
-local matrix row 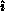 using the row data
distribution function. Having identified themselves, the pivot-row processes
can look for the largest element in local matrix row
using the row data
distribution function. Having identified themselves, the pivot-row processes
can look for the largest element in local matrix row 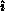 and choose
the pivot element globally among themselves via a combine. At
completion, this places
and choose
the pivot element globally among themselves via a combine. At
completion, this places 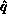 ,
, 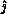 , and the pivot value in the
entire pivot process row. This completes the requirements for the ``first row
fanout'' correctness mode. For preset pivoting, the kelimination row
and column are both stored as
, and the pivot value in the
entire pivot process row. This completes the requirements for the ``first row
fanout'' correctness mode. For preset pivoting, the kelimination row
and column are both stored as 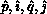 , and
each process knows these values without communication.
, and
each process knows these values without communication. Furthermore, the pivot process looks up the
pivot value. Hence, preset pivoting satisfies the requirements of this
correctness mode also.
Furthermore, the pivot process looks up the
pivot value. Hence, preset pivoting satisfies the requirements of this
correctness mode also.
For ``first row fanout,'' the universal knowledge of 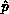 and
knowledge of the pivot matrix row
and
knowledge of the pivot matrix row 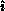 by the pivot process
row, allow the vertical broadcast of this row (new
row of U). In addition, we broadcast
by the pivot process
row, allow the vertical broadcast of this row (new
row of U). In addition, we broadcast 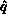 ,
,
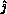 , and the pivot value simultaneously. This extends the
correct value of
, and the pivot value simultaneously. This extends the
correct value of 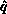 to all processes, as well as
to all processes, as well as  and
the pivot value to the pivot process column. Hence, the multiplier
(L) column may be correctly computed and broadcast .
Along with the multiplier column broadcast , we include
the pivot value. After this broadcast , all processes
have the correct indices
and
the pivot value to the pivot process column. Hence, the multiplier
(L) column may be correctly computed and broadcast .
Along with the multiplier column broadcast , we include
the pivot value. After this broadcast , all processes
have the correct indices 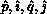 and
the pivot value. This provides all that's required to complete the
current elimination step.
and
the pivot value. This provides all that's required to complete the
current elimination step.
For the second correctness mode ``first column fanout,'' the exit conditions
for the pivot function are: All processes must know 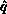 and the entire
pivot process column must know
and the entire
pivot process column must know 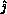 , the pivot value, and
, the pivot value, and 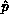 .
The pivot process in addition knows
.
The pivot process in addition knows 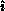 . Partial row pivoting can
be set up to satisfy these correctness conditions. The arguments are
analogous to partial column pivoting and are given in [Skjellum:90c].
. Partial row pivoting can
be set up to satisfy these correctness conditions. The arguments are
analogous to partial column pivoting and are given in [Skjellum:90c].
For ``first column fanout,'' the entire pivot process column knows the
pivot value, and local column of the pivot. Hence, the multiplier
column may be computed by dividing the pivot matrix column by the pivot
value. This column of L can then be broadcast
horizontally, including the pivot value, 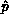 , and
, and 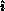 as
additional information. After this step, the entire ensemble has the
correct pivot value, and
as
additional information. After this step, the entire ensemble has the
correct pivot value, and 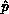 ; in addition, the pivot process row
has the correct
; in addition, the pivot process row
has the correct 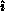 . Hence, the pivot matrix row may be
identified and broadcast . This second
broadcast completes the needed information in each
process for effecting the kelimination step.
. Hence, the pivot matrix row may be
identified and broadcast . This second
broadcast completes the needed information in each
process for effecting the kelimination step.
Thus, when using partial row or partial column pivoting, only local
combines of the pivot process column (respectively row) are needed.
The other processes don't participate in the combine, as they must
without this methodology. Preset pivoting implies no pivoting
communication, except very occasionally (e.g., 1 in 5000 times),
as noted in [Skjellum:90c], to remove memory unscalabilities. This
pivoting approach is a direct savings, gained at a negligible
additional broadcast overhead. See also
[Skjellum:90c].





Next: 9.5.4 New Data Distributions
Up: LU Factorization of
Previous: 9.5.2 Design Overview
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
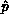 (the pivot process row); the
pivot process row must know
(the pivot process row); the
pivot process row must know 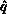 (the pivot process column) as well as
(the pivot process column) as well as
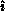 , the
, the 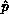 -local matrix row of the pivot; and the pivot
process must know in addition the pivot value and
-local matrix row of the pivot; and the pivot
process must know in addition the pivot value and 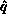 -local matrix
column
-local matrix
column 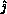 of the pivot. Partial column pivoting and preset
pivoting can be set up to satisfy these correctness conditions as follows. For
partial column pivoting, the krow is eliminated at the kstep of
the factorization. From this fact, each process can derive the process row
of the pivot. Partial column pivoting and preset
pivoting can be set up to satisfy these correctness conditions as follows. For
partial column pivoting, the krow is eliminated at the kstep of
the factorization. From this fact, each process can derive the process row
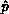 and
and  -local matrix row
-local matrix row 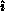 using the row data
distribution function. Having identified themselves, the pivot-row processes
can look for the largest element in local matrix row
using the row data
distribution function. Having identified themselves, the pivot-row processes
can look for the largest element in local matrix row 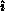 and choose
the pivot element globally among themselves via a combine. At
completion, this places
and choose
the pivot element globally among themselves via a combine. At
completion, this places 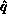 ,
, 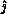 , and the pivot value in the
entire pivot process row. This completes the requirements for the ``first row
fanout'' correctness mode. For preset pivoting, the kelimination row
and column are both stored as
, and the pivot value in the
entire pivot process row. This completes the requirements for the ``first row
fanout'' correctness mode. For preset pivoting, the kelimination row
and column are both stored as 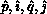 , and
each process knows these values without communication.
, and
each process knows these values without communication. Furthermore, the pivot process looks up the
pivot value. Hence, preset pivoting satisfies the requirements of this
correctness mode also.
Furthermore, the pivot process looks up the
pivot value. Hence, preset pivoting satisfies the requirements of this
correctness mode also.





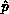 and
knowledge of the pivot matrix row
and
knowledge of the pivot matrix row 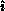 by the pivot process
row, allow the vertical broadcast
by the pivot process
row, allow the vertical broadcast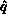 ,
,
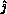 , and the pivot value simultaneously. This extends the
correct value of
, and the pivot value simultaneously. This extends the
correct value of 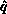 to all processes, as well as
to all processes, as well as  and
the pivot value to the pivot process column. Hence, the multiplier
(L) column may be correctly computed and broadcast
and
the pivot value to the pivot process column. Hence, the multiplier
(L) column may be correctly computed and broadcast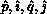 and
the pivot value. This provides all that's required to complete the
current elimination step.
and
the pivot value. This provides all that's required to complete the
current elimination step.
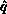 and the entire
pivot process column must know
and the entire
pivot process column must know 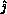 , the pivot value, and
, the pivot value, and 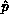 .
The pivot process in addition knows
.
The pivot process in addition knows 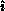 . Partial row pivoting can
be set up to satisfy these correctness conditions. The arguments are
analogous to partial column pivoting and are given in [
. Partial row pivoting can
be set up to satisfy these correctness conditions. The arguments are
analogous to partial column pivoting and are given in [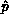 , and
, and 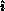 as
additional information. After this step, the entire ensemble has the
correct pivot value, and
as
additional information. After this step, the entire ensemble has the
correct pivot value, and 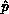 ; in addition, the pivot process row
has the correct
; in addition, the pivot process row
has the correct 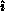 . Hence, the pivot matrix row may be
identified and broadcast
. Hence, the pivot matrix row may be
identified and broadcast