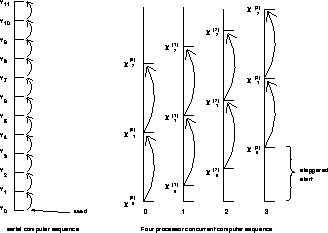
Figure 7.13: A Comparison of the Sequential and Concurrent Generation of Random Numbers





Many important algorithms in science and engineering are of the Monte Carlo type. This means that they employ pseudorandom number generators to simulate physical systems which are inherently probabilistic or statistical in nature. At other times, Monte Carlo is used to getting a fast approximation to what is actually a large, deterministic computation. Examples of this are Lattice Gauge computations (Section 4.3) and Simulated Annealing methods (Sections 11.1.4 and 11.4).

Figure 7.13: A Comparison of the Sequential and Concurrent Generation of
Random Numbers
Even for a sequential algorithm, the question of correlations between members of the pseudorandom number sequence is nontrivial. In the parallel case, at least for the popular linear congruential algorithm, it is easy for the parallel algorithm to exactly mimic what a sequential algorithm would do. This means that the parallel case can be reduced to the well-understood sequential case.
The fundamental idea is that the processors of an N processor concurrent computer each compute only the Nnumber of the sequential random number sequence. The parallel sequences are staggered and interleaved so that the parallel computer exactly reproduces the sequential sequence. Figure 7.13 illustrates what happens in the parallel case versus the sequential case for a four-processor concurrent computer.
Chapter 12 of [Fox:88a] has an extensive discussion of the parallel algorithm. This reference also has a discussion of what to do to achieve exact matching between parallel and sequential computations in more complex applications. We extend this work from the linear congruential method of [Fox:88a] to the so-called shift register sequences, which have longer periods and less correlations than the congruential method [Chiu:88b], [Ding:88d]. As an illustration, we use Ding's Fibonacci additive random number generator developed for the QCD calculations on the Mark IIIfp, as previously described in Section 4.3. This uses the sequence
This has a period longer than 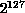 . The assembly language code
for Equation 7.12 on the Mark IIIfp took
. The assembly language code
for Equation 7.12 on the Mark IIIfp took 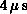 to generate a floating-point random number normalized to the range [0,1).
to generate a floating-point random number normalized to the range [0,1).




