




Next: Theoretical Interpretation
Up: 6.4.1 The case of
Previous: Origin of the
For the large anisotropy system, h=1, the specific heat 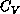 are shown for
several spin systems in Figure 6.15(a). The peak becomes sharper
and higher as the system size increases, indicating a divergent peak in an
infinite system, similar to the two-dimensional Ising model. Defining the
transition temperature
are shown for
several spin systems in Figure 6.15(a). The peak becomes sharper
and higher as the system size increases, indicating a divergent peak in an
infinite system, similar to the two-dimensional Ising model. Defining the
transition temperature 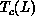 at the peak of
at the peak of 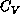 for the finite
for the finite
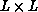 system, the finite-size scaling theory [Landau:76a] predicts
that
system, the finite-size scaling theory [Landau:76a] predicts
that 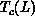 relates to
relates to 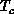 through the scaling law
through the scaling law
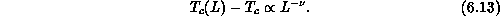
Setting 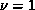 , the Ising exponent, a good fit with
, the Ising exponent, a good fit with 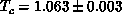 , is
shown in Figure 6.15(b). A different scaling with the same
exponent for the correlation length,
, is
shown in Figure 6.15(b). A different scaling with the same
exponent for the correlation length,
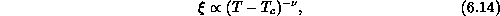
is also satisfied quite well, resulting in 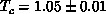 . The
staggered magnetization drops down near
. The
staggered magnetization drops down near 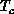 , although the behaviors are
rounded off on these finite-size systems. All the evidence clearly
indicates that an Ising-like antiferromagnetic transition occurs at
, although the behaviors are
rounded off on these finite-size systems. All the evidence clearly
indicates that an Ising-like antiferromagnetic transition occurs at 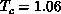 , with a divergent specific heat. In the smaller anisotropy case,
, with a divergent specific heat. In the smaller anisotropy case,
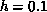 , similar behaviors are found. The scaling for the correlation length
is shown in Figure 6.16, indicating a transition at
, similar behaviors are found. The scaling for the correlation length
is shown in Figure 6.16, indicating a transition at 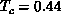 .
However, the specific heat remains finite at all temperatures.
.
However, the specific heat remains finite at all temperatures.
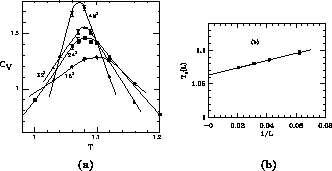
Figure 6.15: (a) The Specific Heat for Different Size Systems of h=1. (b)
Finite Size Scaling for 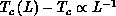 .
.
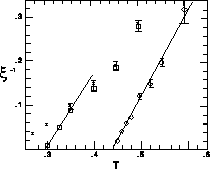
Figure 6.16: The Inverse Correlation Lengths for 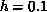 System
(
System
( ),
), 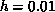 System (
System ( ), and h=0 System
(
), and h=0 System
( ) for the Purpose of Comparison. The straight lines are the
scaling relation:
) for the Purpose of Comparison. The straight lines are the
scaling relation: 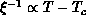 . From it we can pin down
. From it we can pin down
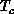 .
.
The most interesting case is 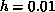 (or
(or 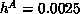 , very close to those
in
, very close to those
in 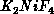 [Birgeneau:71a]). Figure 6.17 shows the
staggered correlation function at
[Birgeneau:71a]). Figure 6.17 shows the
staggered correlation function at 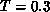 compared with those on the
isotropic model [Ding:90g]. The inverse correlation length measured,
together with those for the isotropic model (h=0), are shown in
Figure 6.16. Below
compared with those on the
isotropic model [Ding:90g]. The inverse correlation length measured,
together with those for the isotropic model (h=0), are shown in
Figure 6.16. Below 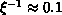 , the Ising behavior of
a straight line becomes clear. Clearly, the system becomes
antiferromagnetically ordered around
, the Ising behavior of
a straight line becomes clear. Clearly, the system becomes
antiferromagnetically ordered around 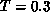 . The best estimate is
. The best estimate is
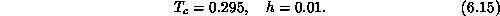
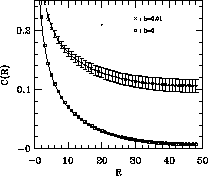
Figure 6.17: The Correlation Function on the 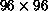 System at
System at 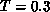 for
for 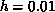 system. It decays with correlation length
system. It decays with correlation length 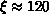 . Also shown is the isotropic case h=0, which has
. Also shown is the isotropic case h=0, which has 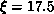 .
.





Next: Theoretical Interpretation
Up: 6.4.1 The case of
Previous: Origin of the
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
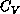 are shown for
several spin systems in Figure 6.15(a). The peak becomes sharper
and higher as the system size increases, indicating a divergent peak in an
infinite system, similar to the two-dimensional Ising model. Defining the
transition temperature
are shown for
several spin systems in Figure 6.15(a). The peak becomes sharper
and higher as the system size increases, indicating a divergent peak in an
infinite system, similar to the two-dimensional Ising model. Defining the
transition temperature 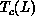 at the peak of
at the peak of 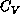 for the finite
for the finite
 system, the finite-size scaling theory [Landau:76a] predicts
that
system, the finite-size scaling theory [Landau:76a] predicts
that 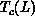 relates to
relates to 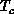 through the scaling law
through the scaling law





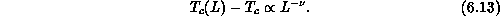
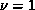 , the Ising exponent, a good fit with
, the Ising exponent, a good fit with 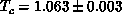 , is
shown in Figure
, is
shown in Figure 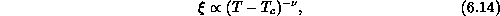
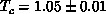 . The
staggered magnetization drops down near
. The
staggered magnetization drops down near 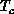 , although the behaviors are
rounded off on these finite-size systems. All the evidence clearly
indicates that an Ising-like antiferromagnetic transition occurs at
, although the behaviors are
rounded off on these finite-size systems. All the evidence clearly
indicates that an Ising-like antiferromagnetic transition occurs at 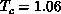 , with a divergent specific heat. In the smaller anisotropy case,
, with a divergent specific heat. In the smaller anisotropy case,
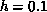 , similar behaviors are found. The scaling for the correlation length
is shown in Figure
, similar behaviors are found. The scaling for the correlation length
is shown in Figure 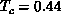 .
However, the specific heat remains finite at all temperatures.
.
However, the specific heat remains finite at all temperatures.

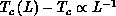 .
.
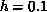 System
(
System
( ),
), 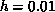 System (
System ( ), and h=0 System
(
), and h=0 System
( ) for the Purpose of Comparison. The straight lines are the
scaling relation:
) for the Purpose of Comparison. The straight lines are the
scaling relation: 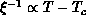 . From it we can pin down
. From it we can pin down
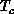 .
.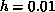 (or
(or 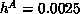 , very close to those
in
, very close to those
in 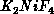 [
[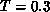 compared with those on the
isotropic model [
compared with those on the
isotropic model [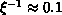 , the Ising behavior of
a straight line becomes clear. Clearly, the system becomes
antiferromagnetically ordered around
, the Ising behavior of
a straight line becomes clear. Clearly, the system becomes
antiferromagnetically ordered around 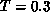 . The best estimate is
. The best estimate is
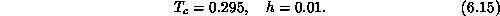

 System at
System at 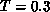 for
for 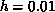 system. It decays with correlation length
system. It decays with correlation length 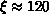 . Also shown is the isotropic case h=0, which has
. Also shown is the isotropic case h=0, which has 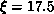 .
.