




Next: Simulation Results
Up: 6.4.1 The case of
Previous: 6.4.1 The case of
In the antiferromagnetic spin system, superexchange leads to the dominant
isotropic coupling. One of the high-order effects, due to
crystal field, is written as 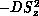 , which is a constant for these
spin-
, which is a constant for these
spin-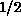 high-
high-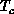 materials. Another second-order effect is the
spin-orbital coupling. This effect will pick up a preferred direction and
lead to an
materials. Another second-order effect is the
spin-orbital coupling. This effect will pick up a preferred direction and
lead to an 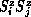 term, which also arises due to the lattice distortion
in
term, which also arises due to the lattice distortion
in 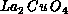 . More complicated terms, like the antisymmetric exchange,
can also be generated. For simplicity and clarity, we focus the study on the
antiferromagnetic Heisenberg model with an Ising-like anisotropy as in
Equation 6.12. The anisotropy parameter h relates to the usual
reduced anisotropy energy
. More complicated terms, like the antisymmetric exchange,
can also be generated. For simplicity and clarity, we focus the study on the
antiferromagnetic Heisenberg model with an Ising-like anisotropy as in
Equation 6.12. The anisotropy parameter h relates to the usual
reduced anisotropy energy 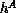 through
through 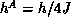 . In the past, the
anisotropy field model,
. In the past, the
anisotropy field model, 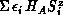 , has also been
included. However, its origin is less clear and, furthermore, the
Ising symmetry is explicitly broken.
, has also been
included. However, its origin is less clear and, furthermore, the
Ising symmetry is explicitly broken.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
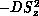 , which is a constant for these
spin-
, which is a constant for these
spin-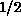 high-
high-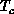 materials. Another second-order effect is the
spin-orbital coupling. This effect will pick up a preferred direction and
lead to an
materials. Another second-order effect is the
spin-orbital coupling. This effect will pick up a preferred direction and
lead to an 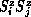 term, which also arises due to the lattice distortion
in
term, which also arises due to the lattice distortion
in 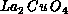 . More complicated terms, like the antisymmetric exchange,
can also be generated. For simplicity and clarity, we focus the study on the
antiferromagnetic Heisenberg model with an Ising-like anisotropy as in
Equation 6.12. The anisotropy parameter h relates to the usual
reduced anisotropy energy
. More complicated terms, like the antisymmetric exchange,
can also be generated. For simplicity and clarity, we focus the study on the
antiferromagnetic Heisenberg model with an Ising-like anisotropy as in
Equation 6.12. The anisotropy parameter h relates to the usual
reduced anisotropy energy 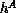 through
through 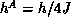 . In the past, the
anisotropy field model,
. In the past, the
anisotropy field model, 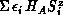 , has also been
included. However, its origin is less clear and, furthermore, the
Ising symmetry is explicitly broken.
, has also been
included. However, its origin is less clear and, furthermore, the
Ising symmetry is explicitly broken.




