Glossary

 

The following is a glossary of terms and notation used throughout this users guide and the leading comments of the source code. The first time notation from this glossary appears in the text, it will be italicized.

• Array descriptor: Contains the information required to establish the mapping between a global matrix entry and its corresponding process and memory location  .

  The notations x_ used in the entries of the array descriptor denote the attributes of a global matrix. For example, M_ denotes the number of rows, and M_A specifically denotes the number of rows in global matrix A. See sections 4.2,  4.3.3,  4.4.5,  4.4.6, and  4.5.1 for complete details.

• BLACS : Basic Linear Algebra Communication Subprograms, a message-passing library designed for linear algebra. They provide a portability layer for communication between ScaLAPACK and message-passing systems such as MPI and PVM, as well as native message-passing libraries such as NX and MPL. See section 1.3.4.
• BLAS : Basic Linear Algebra Subprograms [57, 59, 93], a standard for subroutines for common linear algebra computations such as dot-products, matrix-vector multiplication, and matrix-matrix multiplication. They provide a portability layer for computation. See section 1.3.2.
• Block size: The number of contiguous rows or columns of a global matrix to be distributed consecutively to each of the processes in the process grid. The block size is quantified by the notation , where MB is the row block size and NB is the column block size.

  The distribution block size can be square, MB=NB, or rectangular, . Block size  is also referred to as the partitioning unit  or blocking factor .

• Distributed memory computer: A term used in two senses:
  • A computer marketed as a distributed memory computer (such as the Cray T3 computers, the IBM SP computers, or the Intel Paragon), including one or more message-passing libraries.
  • A distributed shared-memory computer (e.g., the Origin 2000) or network of workstations (e.g., the Berkeley NOW) with message passing.
  ScaLAPACK delivers high performance on these computers provided that they include certain key features such as an efficient message-passing system, a one-to-one mapping of processes to processors, a gang scheduler and a well-connected communication network.
• Distribution : Method by which the entries of a global matrix are allocated among the processes, also commonly referred to as decomposition   or data layout . Examples of distributions used by ScaLAPACK include block and block-cyclic distributions and these will be illustrated and explained in detail later.

  Data distribution in ScaLAPACK is controlled primarily by the process grid and the block size.

• Global: A term ``global''   used in two ways:
  • To define the mathematical matrix , e.g. the global matrix A.
  • To identify arguments that must have the same value on all processes .
• (K_) : Number of columns that a process receives if columns of a matrix are distributed over c columns of its process row.

  To be consistent in notation, we have used a ``modifying character'' subscript on LOC to denote the dimension of the process grid to which we are referring. The subscript ``r'' indicates ``row'' whenever it is appended to LOC; likewise, the subscript ``c'' indicates ``column'' when it is appended to LOC.

  The value of () may differ from process to process within the process grid. For example, in figure 4.6 (section 4.3.4), we can see that for process (0,0) (N_)= 4; however, for process (0,1) (N_) = 3.

• (K_) : Number of rows that a process would receive if rows of a matrix are distributed over r rows of its process column.

  To be consistent in notation, we have used a ``modifying character'' subscript on LOC to denote the dimension of the process grid to which we are referring. The subscript ``r'' indicates ``row'' whenever it is appended to LOC; likewise, the subscript ``c'' indicates ``column'' when it is appended to LOC.

  The value of () may differ from process to process within the process grid. For example, in figure 4.6 (section 4.3.4), we can see that for process (0,0) (M_)= 5; however, for process (1,0) (M_) = 4.

• Local: A term    used in two ways:
  • To express the array elements or blocks stored on each process, e.g., the local part of the global matrix A, also referred to as the local array . The size of the local array may differ from process to process. See section 2.3 for further details.
  • To identify arguments that may have different values on different processes. 

• Local leading dimension   of a local array: Specification of entry size for local array. When a global array is distributed among the processes in the process grid, locally the entries are stored in a two-dimensional array, the size of which may vary from process to process. Thus, a leading dimension needs to be specified for each local array. For example, in Figure 2.2 in section 2.3, we can see that for process (0,0) the local leading dimension of the local array A (denoted ) is 5, whereas for process (1,0) the local leading dimension of local array A is 4.
• MYCOL : The calling process's column coordinate in the process grid. Each process within the process grid is uniquely identified by its process coordinates (MYROW, MYCOL).
• MYROW : The calling process's row coordinate in the process grid. Each process within the process grid is uniquely identified by its process coordinates (MYROW, MYCOL).
• P : The total number of processes in the process grid, i.e., .

  In terms of notation for process grids, we have used a ``modifying character'' subscript on P to denote the dimension of the process grid to which we are referring. The subscript ``r'' indicates ``row'' whenever it is appended to P, and thus is the number of process rows in the process grid. Likewise, the subscript ``c'' indicates ``column'' when it is appended to P, and thus is the number of process columns in the process grid.

•  : The number of process columns in the process grid (i.e., the second dimension of the two-dimensional process grid).
•  : The number of process rows in the process grid (i.e., the first dimension of the two-dimensional process grid).
• PBLAS : A distributed-memory version of the BLAS (Basic Linear Algebra Subprograms), also referred to as the Parallel BLAS or Parallel Basic Linear Algebra Subprograms. Refer to section 1.3.3 for further details.
• Process: Basic unit or thread of execution  that minimally includes a stack, registers, and memory. Multiple processes may share a physical processor. The term processor  refers to the actual hardware.

  In ScaLAPACK, each process is treated as if it were a processor: the process must exist for the lifetime of the ScaLAPACK run, and its execution should affect other processes' execution only through the use of message-passing calls. With this in mind, we use the term process in all sections of this users guide except those dealing with timings. When discussing timings, we specify processors as our unit of execution, since speedup will be determined largely by actual hardware resources.

  In ScaLAPACK, algorithms are presented in terms of processes, rather than physical processors. In general there may be several processes on a processor, in which case we assume that the runtime system handles the scheduling of processes. In the absence of such a runtime system, ScaLAPACK assumes one process per processor.

• Process column : A specific column of processes within the two-dimensional process grid. For further details, consult the definition of process grid.
• Process grid  : The way we logically view a parallel machine as a one- or two-dimensional rectangular grid of processes.

  For two-dimensional process grids, the variable   is used to indicate the number of rows in the process grid (i.e., the first dimension of the two-dimensional process grid). The variable   is used to indicate the number of columns in the process grid (i.e., the second dimension of the two-dimensional process grid). The collection of processes need not physically be connected in the two-dimensional process grid.

  For example, the following figure shows six processes mapped to a grid, where and .

  

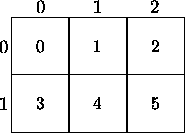
  A user may perform an operation within a process row or process column of the process grid. A process row refers to a specific row of processes within the process grid, and a process column refers to a specific column of processes with the process grid. In the example, process row 0 contains the processes with natural ordering 0, 1, and 2, and process column 0 contains the processes with natural ordering 0 and 3.

  For further details, please refer to section 4.1.1.

• Process row : A specific row of processes within the two-dimensional process grid. For further details, consult the definition of process grid.
• Scope : A term used in two ways:
  • The portion of the process grid within which an operation is defined. For example, in the Level 1 PBLAS, the resultant output array or scalar will be global or local within a process column or row of the process grid, and undefined elsewhere .
    

    Equivalently, in Appendix D.3, scope indicates the processes that participate in the broadcast or global combine operations. Scope can equal ``all'', ``row'', or ``column'' .

  • The portion of the parallel program within which the definition of an argument remains unchanged. When the scope of an argument is defined as global , the argument must have the same value on all processes. When the scope of an argument is defined as local , the argument may have different values on different processes .
  Refer to section 4.1.3 for further details.