




Next: Example (from Program LA_SPSVX_EXAMPLE)
Up: Symmetric Indefinite Linear Systems
Previous: Description
Contents
Index
- AP
- (input) REAL or COMPLEX array,
shape
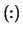 with
with
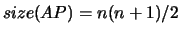 , where
, where 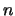 is the order
of
is the order
of  .
.
On entry, the upper or lower triangle of matrix  in packed storage. The
elements are stored columnwise as follows:
in packed storage. The
elements are stored columnwise as follows:
- B
- (input) REAL or COMPLEX array, shape
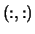 with
with
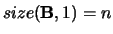 or shape
or shape 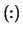 with
with
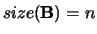 .
.
The matrix 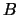 .
.
- X
- (output) REAL or COMPLEX array, shape
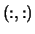 with
with
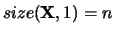 and
and
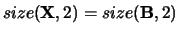 , or shape
, or shape 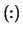 with
with
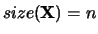 .
.
The solution matrix 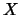 .
.
- UPLO
- Optional (input) CHARACTER(LEN=1).
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
Default value: 'U'.
- AFP
- Optional (input or output) REAL
or COMPLEX array, shape
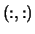 with the same size as AP.
with the same size as AP.
If FACT = 'F', then AFP is an input argument that
contains the block diagonal matrix  and the multipliers used to
obtain the factor
and the multipliers used to
obtain the factor 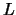 or
or 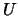 from the factorization of
from the factorization of  , returned by
a previous call to LA_SPSVX or LA_HPSVX and stored as a packed
triangular matrix in the same storage format as
, returned by
a previous call to LA_SPSVX or LA_HPSVX and stored as a packed
triangular matrix in the same storage format as  .
.
If FACT = 'N', then AFP is an output argument that
contains the block diagonal matrix  and the multipliers used to
obtain the factor
and the multipliers used to
obtain the factor 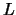 or
or 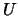 from the factorization of
from the factorization of  , stored as a packed
triangular matrix in the same storage format as
, stored as a packed
triangular matrix in the same storage format as  .
.
- IPIV
- Optional (input or output) INTEGER array,
shape
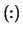 with
with
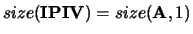 .
.
If FACT = 'F', then 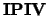 is an input argument that
contains details of the row and column interchanges and the block
structure of
is an input argument that
contains details of the row and column interchanges and the block
structure of  .
.
![\begin{optionarg}
\item[{If ${\bf IPIV}_k > 0$}], then rows and columns $k$\ an...
...:k+1,k:k+1}$\ is a $2\times 2$\ diagonal block.
\end{numbersec} \end{optionarg}](img492.gif)
If FACT = 'N', then IPIV is an output argument and on exit
contains details of the interchanges and the block structure of  (as described above).
(as described above).
- FACT
- Optional (input) CHARACTER(LEN=1).
Specifies whether the factored form of  has been supplied on entry.
has been supplied on entry.
![\begin{optionarg}
\item[{$ = $\ 'N':}] The matrix $A$\ will be copied to {\bf A...
...] {\bf AFP} and ${\bf IPIV}$\ contain the factored
form of $A$.
\end{optionarg}](img510.gif)
Default value: 'N'.
- FERR
- Optional (output) REAL array
of shape
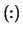 , with
, with
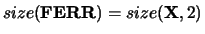 , or REAL scalar.
, or REAL scalar.
The estimated forward error bound for each solution vector
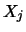 (the
(the 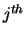 column of the solution matrix
column of the solution matrix 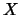 ).
If
).
If 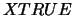 is the true solution corresponding to
is the true solution corresponding to 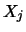 ,
, 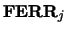 is an estimated upper bound for the magnitude of the largest
element in (
is an estimated upper bound for the magnitude of the largest
element in (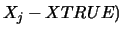 divided by the magnitude of the
largest element in
divided by the magnitude of the
largest element in 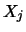 . The estimate is as reliable as
the estimate for
. The estimate is as reliable as
the estimate for 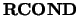 , and is almost always a slight
overestimate of the true error.
, and is almost always a slight
overestimate of the true error.
- BERR
- Optional (output) REAL array
of shape
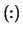 , with
, with
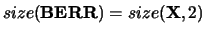 , or REAL scalar.
, or REAL scalar.
The componentwise relative backward error of each solution
vector 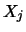 (i.e., the smallest relative change in
any element of
(i.e., the smallest relative change in
any element of  or
or 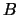 that makes
that makes 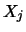 an exact solution).
an exact solution).
- RCOND
- Optional (output) REAL
The estimate of the reciprocal condition number of
 . If
. If 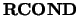 is less than the machine precision, the matrix
is singular to working precision. This condition is
indicated by a return code of
is less than the machine precision, the matrix
is singular to working precision. This condition is
indicated by a return code of
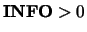 .
.
- INFO
- (output) INTEGER
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...\bf RCOND} would suggest.
\end{infoarg}$n$\ is the order of $A$.
\end{infoarg}](img494.gif)
If 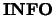 is not present and an error occurs, then the program is
terminated with an error message.
is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20,21].





Next: Example (from Program LA_SPSVX_EXAMPLE)
Up: Symmetric Indefinite Linear Systems
Previous: Description
Contents
Index
Susan Blackford
2001-08-19
![\begin{optionarg}
\item[{$=$\ 'U':}] Upper triangle of $A$\ is stored;
\item[{$=$\ 'L':}] Lower triangle of $A$\ is stored.
\end{optionarg}](img443.gif)
![\begin{optionarg}
\item[{If ${\bf IPIV}_k > 0$}], then rows and columns $k$\ an...
...:k+1,k:k+1}$\ is a $2\times 2$\ diagonal block.
\end{numbersec} \end{optionarg}](img492.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if ${\bf IN...
...\bf RCOND} would suggest.
\end{infoarg}$n$\ is the order of $A$.
\end{infoarg}](img494.gif)