




Next: Arguments
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
-
30.
- If FACT = 'N', a diagonal pivoting method is used to
factor the matrix
 as
as
or
where U (or L) is a product of permutation and unit upper (lower)
triangular matrices, and D is symmetric (LA_SPSVX) or Hermitian (LA_HPSVX)
and block diagonal with 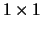 and
and 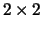 diagonal blocks.
diagonal blocks.
-
31.
- If some
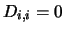 , so that
, so that  is singular, then the routine
returns with
is singular, then the routine
returns with
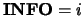 . Otherwise, the factored form of
. Otherwise, the factored form of  is used
to estimate the condition number of the matrix
is used
to estimate the condition number of the matrix  . If the
reciprocal of the condition number is less than machine precision,
. If the
reciprocal of the condition number is less than machine precision,
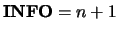 , where
, where 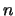 is the order of
is the order of  , is returned as a warning. However, the
routine still goes on to solve for
, is returned as a warning. However, the
routine still goes on to solve for 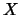 .
Iterative refinement is applied to improve the computed solution.
.
Iterative refinement is applied to improve the computed solution.
-
32.
- LA_SPSVX and LA_HPSVX also optionally compute,
for each solution vector
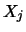 , the estimated
forward error bound and the componentwise relative backward error.
, the estimated
forward error bound and the componentwise relative backward error.





Next: Arguments
Up: Symmetric Indefinite Linear Systems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19