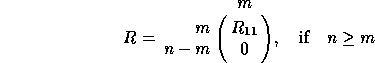
The generalized QR (GQR) factorization of an n-by-m matrix A and an n-by-p matrix B is given by the pair of factorizations
A = QR and B = QTZ
where Q and Z are respectively n-by-n and p-by-p orthogonal matrices (or unitary matrices if A and B are complex). R has the form:
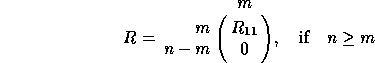
or
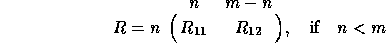
where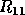 
is upper triangular. T has the form
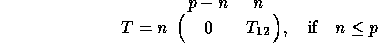
or
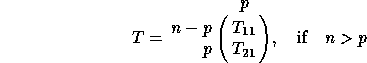
where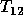 
or 
is upper triangular.
Note that if B is square and nonsingular, the GQR factorization
of A and B implicitly gives the QR factorization of the matrix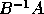 
:
without explicitly computing the matrix inverse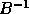 
or the product .
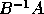The routine xGGQRF computes the GQR factorization by
first computing the QR factorization of A and then
the RQ factorization of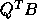 
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or just used to multiply another given matrix
in the same way as the
orthogonal (or unitary) matrix in the QR factorization
(see section 2.3.2).
The GQR factorization was introduced in [63][49]. The implementation of the GQR factorization here follows [2]. Further generalizations of the GQR factorization can be found in [25].
The GQR factorization can be used to solve the general (Gauss-Markov) linear model problem (GLM) (see (2.3) and [60][page 252]GVL2). Using the GQR factorization of A and B, we rewrite the equation d = Ax + By from (2.3) as
We partition this as
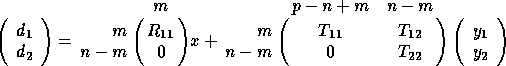
where
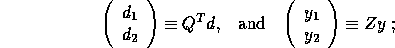
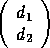can be computed by xORMQR (or xUNMQR).
The GLM problem is solved by setting
from which we obtain the desired solutions
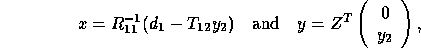
which can be computed by xTRSV, xGEMV and xORMRQ (or xUNMRQ).