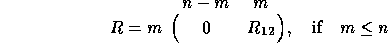
The generalized RQ (GRQ) factorization of an m-by-n matrix A and a p-by-n matrix B is given by the pair of factorizations
A = RQ and B = ZTQ
where Q and Z are respectively n-by-n and p-by-p orthogonal matrices (or unitary matrices if A and B are complex). R has the form
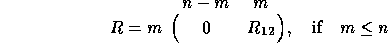
or
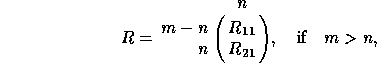
where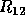 
or 
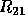is upper triangular. T has the form
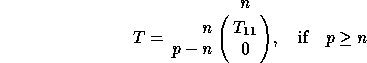
or
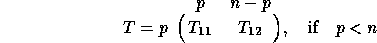
where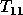 
is upper triangular.
Note that if B is square and nonsingular, the GRQ factorization of
A and B implicitly gives the RQ factorization of the matrix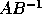 
:
without explicitly computing the matrix inverse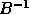 
or the product
.
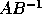The routine xGGRQF computes the GRQ factorization
by first computing the RQ factorization of A and then
the QR factorization of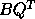 
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the RQ factorization
(see section 2.3.2).
The GRQ factorization can be used to solve the linear equality-constrained least squares problem (LSE) (see (2.2) and [page 567]GVL2). We use the GRQ factorization of B and A (note that B and A have swapped roles), written as
B = TQ and A = ZRQ
We write the linear equality constraints Bx = d as:
TQx = d
which we partition as:
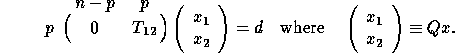
Therefore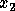 
is the solution of the upper triangular system
Furthermore,
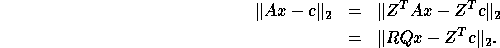
We partition this expression as:
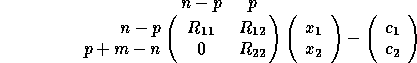
where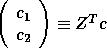 
, which
can be computed by xORMQR (or xUNMQR).
To solve the LSE problem, we set
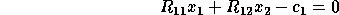
which gives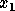 
as the solution of the upper triangular system
Finally, the desired solution is given by
which can be computed by xORMRQ (or xUNMRQ).