




Next: Inexact Rational Krylov Method
Up: Inexact Methods K. Meerbergen
Previous: Jacobi-Davidson Method with Cayley
Contents
Index
Preconditioned Lanczos Method
Suppose that  and
and  are symmetric and that we have a positive
definite
preconditioner
are symmetric and that we have a positive
definite
preconditioner 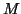 for
for 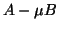 , i.e.,
, i.e.,
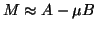 .
We can use the Arnoldi method applied to
.
We can use the Arnoldi method applied to
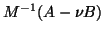 for computing
eigenvalues near
for computing
eigenvalues near 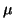 .
(Again, we use a Ritz value
.
(Again, we use a Ritz value 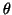 as zero.)
This leads to the recurrence relation
as zero.)
This leads to the recurrence relation
Since 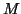 is positive definite, we have that
is positive definite, we have that 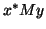 is a valid inner
product.
When we use the
is a valid inner
product.
When we use the 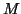 inner product,
inner product, 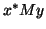 , in the Arnoldi method
rather than
the standard one,
, in the Arnoldi method
rather than
the standard one, 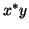 , we have
, we have
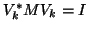 and
and
 ,
so
,
so
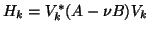 is a symmetric matrix.
This implies that the Arnoldi method with the
is a symmetric matrix.
This implies that the Arnoldi method with the 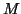 inner product reduces
to
the Lanczos method with
inner product reduces
to
the Lanczos method with 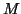 inner product applied to the nonsymmetric
matrix
inner product applied to the nonsymmetric
matrix
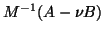 . From earlier discussions,
we conclude that the preconditioned Lanczos method
with
. From earlier discussions,
we conclude that the preconditioned Lanczos method
with 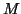 inner product has similar convergence behavior as the
spectral transformation Lanczos method applied to a perturbed problem.
inner product has similar convergence behavior as the
spectral transformation Lanczos method applied to a perturbed problem.
Let 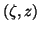 satisfy
satisfy
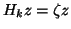 and define the Ritz vector
and define the Ritz vector
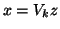 .
This vector is obtained from the Lanczos (Arnoldi) recurrence relation,
so
not from a Galerkin projection.
The Ritz value, on the other hand, can be computed via the Rayleigh
quotient, i.e.,
.
This vector is obtained from the Lanczos (Arnoldi) recurrence relation,
so
not from a Galerkin projection.
The Ritz value, on the other hand, can be computed via the Rayleigh
quotient, i.e.,
which is cheap to compute, e.g. when  is a diagonal matrix.
is a diagonal matrix.
Recall that the Lanczos recurrence relation for the inexact Cayley transform
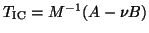 is
is
The recurrence relation can also be written in the form
We know that for a Ritz pair  ,
,
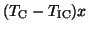 can be
small,
when
can be
small,
when
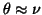 .
So, if
.
So, if 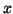 is close to an eigenvector of
is close to an eigenvector of
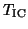 and if
and if
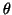 is close to
is close to 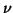 , then
, then 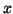 is close to
an eigenvector of
is close to
an eigenvector of
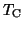 and so the Ritz value
and so the Ritz value 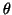 is close to an
eigenvalue of
is close to an
eigenvalue of
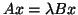 .
.
Morgan and Scott [336] proved the convergence for the following
algorithm, for computing eigenvalues of
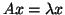 , i.e., with
, i.e., with
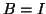 .
.

Note that if 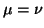 , then the preconditioner must not be a too-good
approximation to
, then the preconditioner must not be a too-good
approximation to 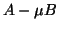 ; otherwise
; otherwise
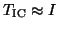 .
The value of
.
The value of 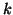 may differ for each
may differ for each 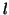 .
Morgan and Scott suggest the stopping test
.
Morgan and Scott suggest the stopping test
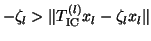 , which is cheap within the
Lanczos method. It is shown in [336] that
if both
, which is cheap within the
Lanczos method. It is shown in [336] that
if both 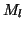 and
and 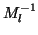 are uniformly bounded in norm,
are uniformly bounded in norm,
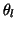 converges to an eigenvalue of
converges to an eigenvalue of  .
Moreover, the asymptotic convergence is quadratic.
.
Moreover, the asymptotic convergence is quadratic.





Next: Inexact Rational Krylov Method
Up: Inexact Methods K. Meerbergen
Previous: Jacobi-Davidson Method with Cayley
Contents
Index
Susan Blackford
2000-11-20
![]() and
and ![]() are symmetric and that we have a positive
definite
preconditioner
are symmetric and that we have a positive
definite
preconditioner ![]() for
for ![]() , i.e.,
, i.e.,
![]() .
We can use the Arnoldi method applied to
.
We can use the Arnoldi method applied to
![]() for computing
eigenvalues near
for computing
eigenvalues near ![]() .
(Again, we use a Ritz value
.
(Again, we use a Ritz value ![]() as zero.)
This leads to the recurrence relation
as zero.)
This leads to the recurrence relation
![]() satisfy
satisfy
![]() and define the Ritz vector
and define the Ritz vector
![]() .
This vector is obtained from the Lanczos (Arnoldi) recurrence relation,
so
not from a Galerkin projection.
The Ritz value, on the other hand, can be computed via the Rayleigh
quotient, i.e.,
.
This vector is obtained from the Lanczos (Arnoldi) recurrence relation,
so
not from a Galerkin projection.
The Ritz value, on the other hand, can be computed via the Rayleigh
quotient, i.e.,
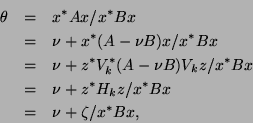
![]() is
is
![]() , i.e., with
, i.e., with
![]() .
.

![]() , then the preconditioner must not be a too-good
approximation to
, then the preconditioner must not be a too-good
approximation to ![]() ; otherwise
; otherwise
![]() .
The value of
.
The value of ![]() may differ for each
may differ for each ![]() .
Morgan and Scott suggest the stopping test
.
Morgan and Scott suggest the stopping test
![]() , which is cheap within the
Lanczos method. It is shown in [336] that
if both
, which is cheap within the
Lanczos method. It is shown in [336] that
if both ![]() and
and ![]() are uniformly bounded in norm,
are uniformly bounded in norm,
![]() converges to an eigenvalue of
converges to an eigenvalue of ![]() .
Moreover, the asymptotic convergence is quadratic.
.
Moreover, the asymptotic convergence is quadratic.