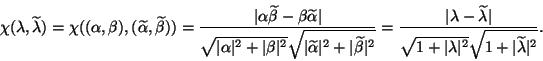In this section, we discuss the tools to assess the accuracy
of computed eigenvalues and corresponding eigenvectors of
the GNHEP of a regular
matrix pair ![]() .
We only assume
the availability of residual vectors which are usually available
upon the exit of a successful computation or cost marginal to compute
afterwards.
For the treatment of error estimation for
the computed eigenvalues, eigenvectors, and deflating subspaces
of dense GNHEPs,
see Chapter 4 of the LAPACK Users' Guide [12].
.
We only assume
the availability of residual vectors which are usually available
upon the exit of a successful computation or cost marginal to compute
afterwards.
For the treatment of error estimation for
the computed eigenvalues, eigenvectors, and deflating subspaces
of dense GNHEPs,
see Chapter 4 of the LAPACK Users' Guide [12].
The situation for general regular pairs ![]() is more
complicated than the standard NHEP
discussed in §7.13 (p.
is more
complicated than the standard NHEP
discussed in §7.13 (p. ![]() ),
especially when
),
especially when ![]() is singular, in which case the
characteristic polynomial
is singular, in which case the
characteristic polynomial
![]() no longer
has degree
no longer
has degree ![]() , the dimension of the matrices
, the dimension of the matrices ![]() and
and ![]() .
Even when
.
Even when ![]() is mathematically
nonsingular but nearly singular, problems arise when one tries to
convert it to a standard eigenvalue problem for
is mathematically
nonsingular but nearly singular, problems arise when one tries to
convert it to a standard eigenvalue problem for ![]() , which then
could have huge eigenvalues and consequently cause numerical instability.
To account for all possibilities, a homogeneous representation
of an eigenvalue
, which then
could have huge eigenvalues and consequently cause numerical instability.
To account for all possibilities, a homogeneous representation
of an eigenvalue ![]() by a nonzero pair of numbers
by a nonzero pair of numbers
![]() has been proposed:
has been proposed:
With this new representation of an eigenvalue, the characteristic polynomial
takes the form
![]() , which does have total degree of
, which does have total degree of
![]() in
in ![]() and
and ![]() . (In fact the
. (In fact the ![]() th term in its expansion is a
multiple of
th term in its expansion is a
multiple of
![]() .)
.)
But how do we measure the difference of two eigenvalues, given the fact of
non-uniqueness in their representations? We resort to
the chordal metric for
![]() and
and
![]() ; their
distance in chordal metric is defined as
; their
distance in chordal metric is defined as