




Next: Error Bound for Computed
Up: Stability and Accuracy Assessments
Previous: Transfer Residual Errors to
Contents
Index
Error Bound for Computed Eigenvalues.
It can be proved [425] that
up to the first order of 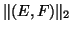 ,
there is an eigenvalue
,
there is an eigenvalue
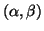 of
of 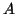 and
and 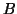 satisfying
satisfying
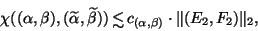 |
(244) |
where
It is called the individual condition number
of
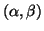 ,
which in actual computations will be estimated with the exact eigenvectors
,
which in actual computations will be estimated with the exact eigenvectors
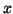 and
and 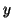 replaced by their approximations
replaced by their approximations 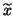 and
and 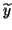 .
.
Susan Blackford
2000-11-20