




Next: Transfer Residual Errors to
Up: Stability and Accuracy Assessments
Previous: Stability and Accuracy Assessments
Contents
Index
Residual Vectors.
Let
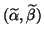 denote a computed eigenvalue, and let
denote a computed eigenvalue, and let
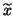 be its corresponding computed eigenvector, i.e.,
be its corresponding computed eigenvector, i.e.,
Sometimes, its corresponding left computed eigenvector
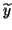 is also available:
is also available:
The residual vectors corresponding to the computed
eigenvalue
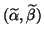 are defined
as
are defined
as
respectively.
For the simplicity, we normalize the
approximate eigenvectors so that
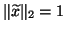 and
and
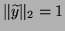 and normalize the approximate eigenvalue so that
and normalize the approximate eigenvalue so that
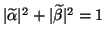 .
.
Susan Blackford
2000-11-20