




Next: Split-and-invert .
Up: Transformation to Standard Problems
Previous: Transformation to Standard Problems
Contents
Index
If  is nonsingular,
then the problem (8.1) is equivalent to
is nonsingular,
then the problem (8.1) is equivalent to
 |
(216) |
where
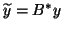 .
Alternatively, the problem (8.1) is also equivalent to
.
Alternatively, the problem (8.1) is also equivalent to
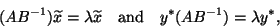 |
(217) |
where
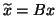 .
If the right eigenvectors are of primary interest, then (8.3) is
preferable, since it avoids an additional back transformation.
.
If the right eigenvectors are of primary interest, then (8.3) is
preferable, since it avoids an additional back transformation.
For an iterative method, as described in Chapter 7,
for the reduced standard eigenvalue problem (8.3)
or (8.4), it is not necessary to evaluate
the product 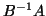 or
or 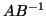 . This is a key observation
in the treatment of large sparse
. This is a key observation
in the treatment of large sparse  and
and  .
One only needs to evaluate matrix-vector products, like
.
One only needs to evaluate matrix-vector products, like
for a given vector 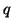 . For a two-sided Lanczos-type method, the vector
. For a two-sided Lanczos-type method, the vector
is also necessary for given vector 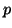 .
Note that the vector
.
Note that the vector
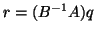 can be computed in two steps:
can be computed in two steps:
(a) form 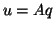 ,
,
(b) solve 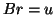 for
for 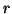 .
.
Similarly, the vector
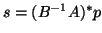 , if necessary, can be evaluated
as
, if necessary, can be evaluated
as
(a)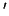 solve
solve 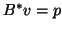 for
for 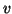 ,
,
(b)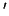 form
form 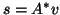 .
.
One can exploit sparsity in each of these steps.
In general, the iterative methods, with the exception of the Jacobi-Davidson
method, require accurate solution of the linear systems at step (b)
(and (b) ). If possible, a direct
linear system solver, say, using LU factorization of
). If possible, a direct
linear system solver, say, using LU factorization of  , is preferable.
See §10.3 for the discussions on dense or sparse
LU factorization.
, is preferable.
See §10.3 for the discussions on dense or sparse
LU factorization.
The error introduced by this transformation to standard form
can be proportional to
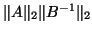 .
If
.
If  is ill-conditioned, then the approach is potentially suspect.
In that situation, one may consider the
SI for the transformation or the
usage of the Jacobi-Davidson method discussed below.
is ill-conditioned, then the approach is potentially suspect.
In that situation, one may consider the
SI for the transformation or the
usage of the Jacobi-Davidson method discussed below.





Next: Split-and-invert .
Up: Transformation to Standard Problems
Previous: Transformation to Standard Problems
Contents
Index
Susan Blackford
2000-11-20
![]() or
or ![]() . This is a key observation
in the treatment of large sparse
. This is a key observation
in the treatment of large sparse ![]() and
and ![]() .
One only needs to evaluate matrix-vector products, like
.
One only needs to evaluate matrix-vector products, like
,
for
.
solve
for
,
form
.
![]() .
If
.
If ![]() is ill-conditioned, then the approach is potentially suspect.
In that situation, one may consider the
SI for the transformation or the
usage of the Jacobi-Davidson method discussed below.
is ill-conditioned, then the approach is potentially suspect.
In that situation, one may consider the
SI for the transformation or the
usage of the Jacobi-Davidson method discussed below.