




Next: Shift-and-Invert.
Up: Transformation to Standard Problems
Previous: Invert .
Contents
Index
In some applications,  is Hermitian positive
definite and well-conditioned.
In this case, it is recommended to compute first a
sparse Cholesky decomposition
is Hermitian positive
definite and well-conditioned.
In this case, it is recommended to compute first a
sparse Cholesky decomposition
with 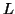 a lower triangular matrix; see §10.3.
The equivalent standard eigenvalue problem is
a lower triangular matrix; see §10.3.
The equivalent standard eigenvalue problem is
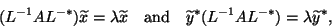 |
(218) |
where
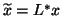 and
and
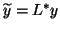 .
As in Invert B, matrices like
.
As in Invert B, matrices like
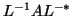 should never be
evaluated explicitly, more in particular because they will in general not
be sparse.
For the application of an iterative method for the standard eigenvalue problem,
we only need to provide the efficient evaluation of
matrix-vector products, like
should never be
evaluated explicitly, more in particular because they will in general not
be sparse.
For the application of an iterative method for the standard eigenvalue problem,
we only need to provide the efficient evaluation of
matrix-vector products, like
or
where 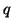 and
and 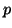 are given vectors.
In practice, the vector
are given vectors.
In practice, the vector
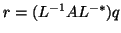 can be formed in three steps:
can be formed in three steps:
(a) solve 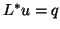 for
for 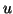 ,
,
(b) form 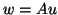 ,
,
(c) solve 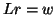 for
for 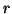 .
.
The vector
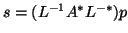 , when necessary,
can be formed as follows:
, when necessary,
can be formed as follows:
(a) solve
solve 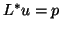 for
for 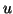 ,
,
(b)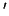 form
form 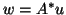 ,
,
(c)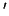 solve
solve 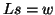 for
for 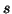 .
.
Since 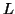 is a triangular matrix, the solutions of linear systems
with
is a triangular matrix, the solutions of linear systems
with 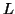 or
or 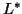 can be obtained
by forward and backward substitutions.
Sparsity can be exploited in a straightforward manner in all these steps.
can be obtained
by forward and backward substitutions.
Sparsity can be exploited in a straightforward manner in all these steps.





Next: Shift-and-Invert.
Up: Transformation to Standard Problems
Previous: Invert .
Contents
Index
Susan Blackford
2000-11-20
for
,
,
for
.
solve
for
,
form
,
solve
for
.