




Next: Solving the Reduced Eigenvalue
Up: Lanczos Method for Complex
Previous: Properties of the Algorithm
Contents
Index
A complete statement of the complex symmetric Lanczos
algorithm (without look-ahead) is as follows.

Next, we comment on a few of the steps of Algorithm 7.17.
- (3)
- If
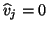 occurs, then the algorithm has fully
exhausted the Krylov sequence generated by
occurs, then the algorithm has fully
exhausted the Krylov sequence generated by  and
and 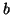 and
thus termination is natural.
In fact, in this case, the Lanczos
vectors generated so far span an
and
thus termination is natural.
In fact, in this case, the Lanczos
vectors generated so far span an  -invariant subspace,
and all eigenvalues of
the Lanczos tridiagonal matrix are also eigenvalues of
-invariant subspace,
and all eigenvalues of
the Lanczos tridiagonal matrix are also eigenvalues of  .
.
- (5)
- In practice, one also needs to stop if a so-called
near breakdown, i.e.,
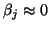 , occurs.
A look-ahead version of the algorithm remedies both
exact breakdowns, i.e.,
, occurs.
A look-ahead version of the algorithm remedies both
exact breakdowns, i.e., 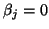 , and near breakdowns;
see, e.g., [178,180].
, and near breakdowns;
see, e.g., [178,180].
- (11)
- To test for convergence, the eigenvalues
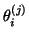 ,
,
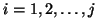 , of the complex
symmetric tridiagonal matrix
, of the complex
symmetric tridiagonal matrix 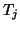 are computed, and the
algorithm is stopped if some of the
are computed, and the
algorithm is stopped if some of the
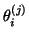 's are
good enough approximations to the desired eigenvalues of
's are
good enough approximations to the desired eigenvalues of  .
.





Next: Solving the Reduced Eigenvalue
Up: Lanczos Method for Complex
Previous: Properties of the Algorithm
Contents
Index
Susan Blackford
2000-11-20
