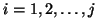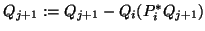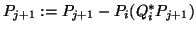Next: An Adaptively Blocked Lanczos
Up: Block Lanczos Methods
Previous: Block Lanczos Methods
Contents
Index
Given an  by
by  matrix
matrix  and initial
and initial  by
by 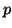 block vectors
block vectors
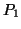 and
and 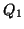 such that
such that
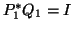 , the block Lanczos method
generates sequences of
, the block Lanczos method
generates sequences of 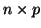 right and left Lanczos block vectors
right and left Lanczos block vectors
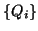 and
and 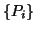 .
These vectors are the biorthonormal bases of the Krylov subspaces
.
These vectors are the biorthonormal bases of the Krylov subspaces
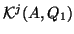 and
and
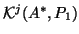 .
Specifically,
after
.
Specifically,
after 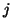 steps, the Lanczos procedure determines a block-tridiagonal matrix
steps, the Lanczos procedure determines a block-tridiagonal matrix
and matrices of right and left Lanczos vectors
that satisfy the biorthonormality condition
![\begin{displaymath}
P^{\ast}_{[j]} Q_{[j]} = I.
\end{displaymath}](img2263.png) |
(155) |
The block Lanczos method uses three-term recurrences
for
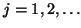 , where
, where 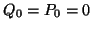 .
In matrix notation, these quantities satisfy the governing relations
.
In matrix notation, these quantities satisfy the governing relations
where 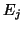 is a
is a 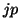 by
by 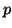 matrix of which the bottom square is
an identity matrix and zeros elsewhere.
matrix of which the bottom square is
an identity matrix and zeros elsewhere.
To use the Lanczos method
for approximating eigenvalues and eigenvectors of  , we solve
the eigenvalue problem of the
, we solve
the eigenvalue problem of the 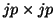 block-tridiagonal matrix
block-tridiagonal matrix ![$T_{[j]}$](img2276.png) .
Each eigentriplet
.
Each eigentriplet
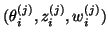 of
of ![$T_{[j]}$](img2276.png) ,
,
determines a Ritz triplet
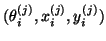 ,
where
,
where
![$x^{(j)}_i = Q_{[j]} z^{(j)}_i$](img2280.png) and
and
![$y^{(j)}_i = P_{[j]} w^{(j)}_i $](img2281.png) .
In general, Ritz triplets approximate outer eigentriplets of
.
In general, Ritz triplets approximate outer eigentriplets of  first.
first.
To assess the approximation,
let 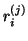 and
and 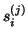 denote the corresponding right and left
residual vectors:
denote the corresponding right and left
residual vectors:
Substitute (7.52) and (7.53), respectively, and there appears
A Ritz value
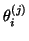 is considered to have converged
if both residual norms are sufficiently small. Similarly,
the residuals can also be used to determine a backward error bound
for the triplet, as in the case for the standard
non-Hermitian Lanczos algorithm (see §7.8).
is considered to have converged
if both residual norms are sufficiently small. Similarly,
the residuals can also be used to determine a backward error bound
for the triplet, as in the case for the standard
non-Hermitian Lanczos algorithm (see §7.8).
A simple blocked version of the basic non-Hermitian Lanczos method is
presented in Algorithm 7.14.

We now comment on some steps of Algorithm 7.14.
- (1)
- The starting vectors
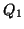 and
and 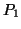 are best selected by the
user to embody any available knowledge concerning
are best selected by the
user to embody any available knowledge concerning  's wanted
eigenvectors. In the absence of such knowledge, choose
's wanted
eigenvectors. In the absence of such knowledge, choose
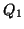 to be a real orthonormalized random
to be a real orthonormalized random 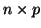 matrix
and let
matrix
and let 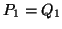 .
.
The block size 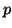 should be chosen to be larger than or equal to the
multiplicity of any wanted eigenvalue. If the multiplicities are
unknown, typical values of
should be chosen to be larger than or equal to the
multiplicity of any wanted eigenvalue. If the multiplicities are
unknown, typical values of 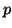 are
are 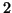 ,
, 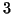 , and
, and 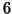 .
.
- (2), (3), (20), (21)
- The user is required to furnish subroutines to calculate the
products
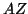 and
and 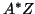 for an arbitrary
for an arbitrary 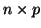 matrix
matrix 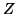 .
This gives the user a chance to calculate these products with only
one pass over the data structure defining
.
This gives the user a chance to calculate these products with only
one pass over the data structure defining  and
and 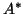 ,
with possible improvements in efficiency.
,
with possible improvements in efficiency.
- (8), (9), (10)
- First, the QR factorizations of
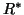 and
and 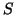 are computed.
If
are computed.
If 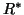 and
and 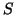 are both of full rank, then
are both of full rank, then
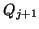 and
and 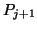 are
are  by
by 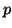 matrices such that
matrices such that
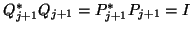 , and both
, and both
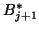 and
and 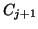 are
are 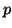 by
by 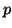 right upper triangular matrices.
If either
right upper triangular matrices.
If either 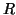 or
or 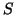 is not of full rank, then an invariant subspace has
been revealed. Continuing the recurrence in the rank-deficient
case is discussed in §7.9.2.
is not of full rank, then an invariant subspace has
been revealed. Continuing the recurrence in the rank-deficient
case is discussed in §7.9.2.
- (12)
- If
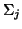 is singular or nearly singular,
that is, if there is a zero or a very tiny singular value, then
there is a breakdown.
Proper action must be taken to continue. See
§7.9.2 for possible treatments.
is singular or nearly singular,
that is, if there is a zero or a very tiny singular value, then
there is a breakdown.
Proper action must be taken to continue. See
§7.9.2 for possible treatments.
- (17), (18)
- The eigentriplets of
![$T_{[j]}$](img2276.png) can be computed
using the method discussed in §7.3.
The convergence of Ritz values can be tested by the norms of
residuals (7.56) and (7.57).
For more details on accessing the accuracy of the approximation,
see § 7.8.2 and §7.13
and [29].
can be computed
using the method discussed in §7.3.
The convergence of Ritz values can be tested by the norms of
residuals (7.56) and (7.57).
For more details on accessing the accuracy of the approximation,
see § 7.8.2 and §7.13
and [29].
When 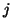 becomes large, solving the eigenproblem of
becomes large, solving the eigenproblem of ![$T_{[j]}$](img2276.png) becomes
time consuming.
A simple way to reduce the cost is to do this periodically,
say every five steps.
becomes
time consuming.
A simple way to reduce the cost is to do this periodically,
say every five steps.
- (19)
- As in the unblocked Lanczos method, in the presence of finite precision
arithmetic, the biorthogonality of the block Lanczos vectors
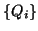 and
and 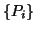 deteriorates. The TSMGS
process can be used to biorthogonalize
deteriorates. The TSMGS
process can be used to biorthogonalize 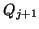 and
and 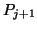 in place
against the previous Lanczos vectors
in place
against the previous Lanczos vectors
![$Q_{[j]} =\left[\, Q_1, Q_2, \ldots, Q_j\, \right]$](img2303.png) and
and
![$P_{[j]} =\left[\, P_1, P_2, \ldots, P_j\, \right]$](img2304.png) .
.
PROCEDURE TSMGS
for 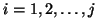
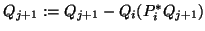
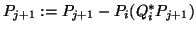
end
- (25)
- This is recommended only if the biorthogonality of the Lanczos vectors is
well maintained. The approximate eigenvectors
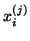 and
and 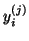 corresponding to converged Ritz
values
corresponding to converged Ritz
values
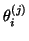 are computed and
the residuals (7.54) and (7.55)
are checked again relative to
are computed and
the residuals (7.54) and (7.55)
are checked again relative to
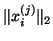 and
and
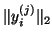 .
Note that the norms can be greater than the estimates computed at step (17).
This is a side-effect of the ill-conditioning of the Lanczos basis vectors.
.
Note that the norms can be greater than the estimates computed at step (17).
This is a side-effect of the ill-conditioning of the Lanczos basis vectors.





Next: An Adaptively Blocked Lanczos
Up: Block Lanczos Methods
Previous: Block Lanczos Methods
Contents
Index
Susan Blackford
2000-11-20
![\begin{displaymath}
T_{[j]} = \left[ \begin{array}{cccc}
A_1 & B_2 & & \\
C_2...
...ts & \ddots & B_j \\
& & C_j & A_j \\
\end{array} \right],
\end{displaymath}](img2261.png)
![\begin{displaymath}
T_{[j]} = \left[ \begin{array}{cccc}
A_1 & B_2 & & \\
C_2...
...ts & \ddots & B_j \\
& & C_j & A_j \\
\end{array} \right],
\end{displaymath}](img2261.png)
![]() , we solve
the eigenvalue problem of the
, we solve
the eigenvalue problem of the ![]() block-tridiagonal matrix
block-tridiagonal matrix ![]() .
Each eigentriplet
.
Each eigentriplet
![]() of
of ![]() ,
,
![]() and
and ![]() denote the corresponding right and left
residual vectors:
denote the corresponding right and left
residual vectors:
![]() should be chosen to be larger than or equal to the
multiplicity of any wanted eigenvalue. If the multiplicities are
unknown, typical values of
should be chosen to be larger than or equal to the
multiplicity of any wanted eigenvalue. If the multiplicities are
unknown, typical values of ![]() are
are ![]() ,
, ![]() , and
, and ![]() .
.
![]() becomes large, solving the eigenproblem of
becomes large, solving the eigenproblem of ![]() becomes
time consuming.
A simple way to reduce the cost is to do this periodically,
say every five steps.
becomes
time consuming.
A simple way to reduce the cost is to do this periodically,
say every five steps.