The primary direct method![]() used in practice to solve the
NHEP (7.1) (and (7.2)) is
the QR algorithm. It first
computes the Schur canonical form (or simply called Schur decomposition)
of a non-Hermitian matrix
used in practice to solve the
NHEP (7.1) (and (7.2)) is
the QR algorithm. It first
computes the Schur canonical form (or simply called Schur decomposition)
of a non-Hermitian matrix ![]() :
:
The QR algorithm is originated from the simple QR iteration:
Let,
For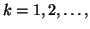
QR-factorize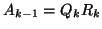
Compute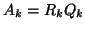
Under certain conditions, ![]() converges to Schur
form
converges to Schur
form ![]() . However, the convergence of the QR iteration is extremely
slow for practical usage. To make QR iteration a fast, effective
method for computing Schur decomposition, a number of crucial
improvements have been developed, including Hessenberg reduction,
implicitly shifting, deflation, and matrix balancing.
We refer the interested reader to
[198,114] and references therein for the details
of the related theory and implementations.
. However, the convergence of the QR iteration is extremely
slow for practical usage. To make QR iteration a fast, effective
method for computing Schur decomposition, a number of crucial
improvements have been developed, including Hessenberg reduction,
implicitly shifting, deflation, and matrix balancing.
We refer the interested reader to
[198,114] and references therein for the details
of the related theory and implementations.
The QR algorithm costs ![]() floating point operations and
floating point operations and ![]() memory for a general
memory for a general
![]() matrix. A crude estimate for the costs
for a real
matrix. A crude estimate for the costs
for a real ![]() matrix is
matrix is ![]() floating point operations if both
floating point operations if both ![]() and
and ![]() are computed.
If only eigenvalues are desired, then about
are computed.
If only eigenvalues are desired, then about ![]() floating point operations are necessary.
floating point operations are necessary.
The QR algorithm is backward stable;
i.e.,
for the computed unitary matrix ![]() (within machine precision)
and the computed upper triangular matrix
(within machine precision)
and the computed upper triangular matrix ![]() , we have
, we have
The subroutine that implements the QR algorithm is
available in almost every
linear algebra-related software package.
It is used as the eig command in
MATLAB.![]() In LAPACK [12],
the following driver routines are available for performing
a variant of tasks for computing Schur decompositions, eigenvalues,
eigenvectors, and estimates for the accuracy of computed results:
In LAPACK [12],
the following driver routines are available for performing
a variant of tasks for computing Schur decompositions, eigenvalues,
eigenvectors, and estimates for the accuracy of computed results:
| xGEES | compute Schur decomposition with eigenvalue ordering, |
| xGEESX | xGEES plus condition estimates, |
| xGEEV | eigenvalues and eigenvectors, |
| xGEEVX | xGEEVX plus condition estimates, |
In ScaLAPACK [52], computational routines are provided for solving the parallel Hessenberg reduction and the parallel QR iteration with implicit shifting. They are PxGEHRD and PxLAHQR, respectively.