Direct Methods

In this section, we briefly discuss methods for computing eigenvalues and eigenvectors of dense matrices. With the factorization (5.4) of $B$, the GHEP (5.1) is reduced to the standard Hermitian eigenproblem (5.5). Then one may use the direct methods discussed in §4.2.

Specifically, in LAPACK [12], the following driver routines are provided for solving the GHEP (5.1) with $B$ positive definite:

• a simple driver xSYGV computes all the eigenvalues and (optionally) eigenvectors. The underlying algorithm is the QR algorithm; see §4.2.
• an expert driver xSYGVX computes all or a selected subset of the eigenvalues and (optionally) eigenvectors. If few enough eigenvalues or eigenvectors are desired, the expert driver is faster than the simple driver. This driver routine uses the QR algorithm or bisection method and inverse iteration, whichever is more efficient.
• a divide-and-conquer driver xSYGVD solves the same problem as the simple driver. It is much faster than the simple driver for large matrices, but uses more workspace. The name divide-and-conquer refers to the underlying divide-and-conquer algorithm; see §4.2.

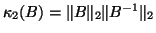Numerical analysis of the methods shows that if $B$ is ill-conditioned with respect to inversion, i.e., the condition number $\kappa_2(B) = \Vert B\Vert _2\Vert B^{-1}\Vert _2$ is large, the methods may be numerically unstable and/or have large errors in computed eigenvalues and eigenvectors. As yet there is no implementation of any direct method directly applicable to $A$ and $B$ while persevering with the symmetry of $A$ and $B$. An alternative approach would be to apply the QZ algorithm (see §8.2), but this will lose the symmetry.