




Next: Transformation to Standard Problems
Up: Generalized Non-Hermitian Eigenvalue Problems
Previous: Introduction
Contents
Index
Direct Methods
The QZ algorithm
is the method of choice for computing the
GNHEP (8.1).
The algorithm is an analog of the
QR algorithm (see §7.3) for the generalized
eigenvalue problem. It follows the pattern described for
the QR algorithm:
 and
and  are first simultaneously reduced to condensed forms by
unitary equivalence transformations. More specifically,
are first simultaneously reduced to condensed forms by
unitary equivalence transformations. More specifically,
 is reduced to upper Hessenberg form and
is reduced to upper Hessenberg form and  is
reduced to upper triangular form (Schur form). The trick is now to
reduce
is
reduced to upper triangular form (Schur form). The trick is now to
reduce  also to upper Schur form, while keeping
also to upper Schur form, while keeping  in that form.
This is accomplished in the next step.
in that form.
This is accomplished in the next step.
- The effect of one shifted QR step on
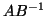 (without forming that
matrix product) is simulated by unitary equivalence transformations
(without forming that
matrix product) is simulated by unitary equivalence transformations
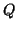 and
and 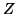 on the matrix pair
on the matrix pair  and
and  ; this is the heart of the
QZ iteration.
If applied iteratively, it reduces
; this is the heart of the
QZ iteration.
If applied iteratively, it reduces  to triangular or
quasi-triangular form (that is, with
to triangular or
quasi-triangular form (that is, with 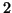 by
by 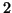 blocks along the
diagonal, in order to avoid complex arithmetic), while preserving the
triangular structure of
blocks along the
diagonal, in order to avoid complex arithmetic), while preserving the
triangular structure of  . At convergence, we have the generalized Schur
form of
. At convergence, we have the generalized Schur
form of  and
and  (see §2.6); that is, we have
computed orthogonal
(see §2.6); that is, we have
computed orthogonal 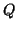 and
and 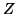 so that
so that 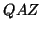 and
and 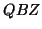 are upper
triangular.
are upper
triangular.
- Eigenvalues can be computed from the diagonals of the triangular
form. Eigenvectors can be computed as the eigenvectors
of the triangular problem and then transformed back with
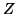 to the
eigenvectors of the original problem.
to the
eigenvectors of the original problem.
This brief sketch has necessarily left a number of important
questions untreated. For more details, the reader should
consult the literature: the original paper on the QZ algorithm
is Moler and Stewart [328]; the QZ algorithm is also
described in the textbooks by, for examples,
Golub and Van Loan [198] or Demmel [114].
The QZ algorithm leads to all eigenvalues and, optionally, to
the right and left eigenvectors.
It requires 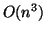 floating point operations and
floating point operations and 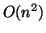 memory locations,
where
memory locations,
where  is the order of
is the order of  and
and  .
More specifically, it requires about
.
More specifically, it requires about 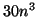 floating point operations for
computing the eigenvalues only.
If right eigenvectors are desired, then an additional
floating point operations for
computing the eigenvalues only.
If right eigenvectors are desired, then an additional 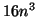 are necessary, and likewise for the left eigenvectors.
These estimates of work are based on the experience
that about two QZ iterations per eigenvalue are sufficient
(the convergence properties of QZ are about the same as for QR).
are necessary, and likewise for the left eigenvectors.
These estimates of work are based on the experience
that about two QZ iterations per eigenvalue are sufficient
(the convergence properties of QZ are about the same as for QR).
Subroutines that implement QZ algorithms are included
in most linear algebra-related software packages.
It is used as the eig(A,B) command in
MATLAB.![[*]](http://www.netlib.org/utk/icons/footnote.png) In LAPACK [12],
the following driver routines are available for performing
a variety of tasks:
In LAPACK [12],
the following driver routines are available for performing
a variety of tasks:
- xGGES: Computes generalized eigenvalues,
the generalized Schur form,
and optionally the left and/or right matrices of Schur vectors.
- xGGESX: xGGES plus condition estimates of eigenvalues
and deflating subspaces.
- xGGEV: Generalized eigenvalues, and optionally
the left and/or right generalized eigenvectors.
- xGGEVX: xGGEV plus condition estimates for
eigenvalues and eigenvectors.
The letter 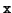 stands for S or D for real single or double
precision
data types, or C or Z for complex single or double precision
data types.
stands for S or D for real single or double
precision
data types, or C or Z for complex single or double precision
data types.





Next: Transformation to Standard Problems
Up: Generalized Non-Hermitian Eigenvalue Problems
Previous: Introduction
Contents
Index
Susan Blackford
2000-11-20
![]() floating point operations and
floating point operations and ![]() memory locations,
where
memory locations,
where ![]() is the order of
is the order of ![]() and
and ![]() .
More specifically, it requires about
.
More specifically, it requires about ![]() floating point operations for
computing the eigenvalues only.
If right eigenvectors are desired, then an additional
floating point operations for
computing the eigenvalues only.
If right eigenvectors are desired, then an additional ![]() are necessary, and likewise for the left eigenvectors.
These estimates of work are based on the experience
that about two QZ iterations per eigenvalue are sufficient
(the convergence properties of QZ are about the same as for QR).
are necessary, and likewise for the left eigenvectors.
These estimates of work are based on the experience
that about two QZ iterations per eigenvalue are sufficient
(the convergence properties of QZ are about the same as for QR).
![]() In LAPACK [12],
the following driver routines are available for performing
a variety of tasks:
In LAPACK [12],
the following driver routines are available for performing
a variety of tasks: