Basic Theory

The Jacobi-Davidson method is based on a combination of two basic principles. The first one is to apply a Galerkin approach for the eigenproblem $A{x}=\lambda {x}$, with respect to some given subspace spanned by an orthonormal basis ${v}_1,\ldots,{v}_m$. The usage of other than Krylov subspaces was suggested by Davidson [99], who also suggested specific choices, different from the ones that we will take, for the construction of orthonormal basis vectors ${v}_j$. The Galerkin condition is

$$AV_m{s}-\theta V_m{s} \perp \{{v}_1, \ldots, {v}_m\} ,$$

which leads to the reduced system

$$V_m^\ast AV_m {s} - \theta {s} = 0 ,$$ (57)

where $V_m$ denotes the matrix with columns ${v}_1$ to ${v}_m$. This equation has $m$ solutions $(\theta_j^{(m)}, {s}_j^{(m)})$. The $m$ pairs $(\theta_j^{(m)}, {u}_j^{(m)}\equiv V_ms_j^{(m)})$ are called the Ritz values and Ritz vectors of ${A}$ with respect to the subspace spanned by the columns of ${V}_m$. These Ritz pairs are approximations for eigenpairs of ${A}$, and our goal is to get better approximations by a well-chosen expansion of the subspace.

At this point the other principle behind the Jacobi-Davidson approach comes into play. The idea goes back to Jacobi [241]. Suppose that we have an eigenvector approximation ${u}_j^{(m)}$ for an eigenvector ${x}$ corresponding to a given eigenvalue $\lambda$. Then Jacobi suggested (in the original paper for strongly diagonally dominant matrices) computing the orthogonal correction ${t}$ for ${u}_j^{(m)}$ so that

$$A({u}_j^{(m)} + {t}) = \lambda ({u}_j^{(m)} +{t}) .$$

Since ${t}\perp {u}_j^{(m)}$, we can restrict ourselves to the subspace orthogonal to ${u}_j^{(m)}$. The operator $A$ restricted to that subspace is given by

$$\left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right)A \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right) ,$$

and we find that ${t}$ satisfies the equation

$$\left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right)(A-\lambda I) \le... ...}_j^{(m)}}^\ast\right){t} = - (A-\theta_j^{(m)} I){u}_j^{(m)} .$$

In practical situations we do not know $\lambda$, and the obvious solution to this is to replace it by its approximation $\theta_j^{(m)}$, which leads to the Jacobi-Davidson correction equation for an update $t_j^{({m})}\perp {u}_j^{(m)}$:

$$\begin{array}{r} \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\rig... ...j^{({m})} \equiv -(A-\theta_j^{(m)}I){u}_j^{(m)}. \end{array}$$ (58)

This correction equation is solved only approximately and its approximate solution $\tilde{t}^{(m)}$ is taken for the expansion of the subspace. This is a fundamental difference with the Krylov subspace methods; instead of selecting a subspace as powers of an operator acting on a given starting vector, we select some subspace without Krylov structure and we project the given matrix onto this subspace.

From (4.48) we conclude that $r_j^{({m})}\perp \{{v}_1, \ldots,{v}_m\}$, and in particular that $r_j^{({m})}\perp {u}_j^{(m)}$, so that the Jacobi-Davidson correction equation represents a consistent linear system.

It can be shown that the exact solution of (4.49) leads to cubic convergence of the largest $\theta_j^{(m)}$ towards $\lambda_{\max}(A)$ for increasing $m$ (similar statements can be made for the convergence towards other eigenvalues of $A$, provided that the Ritz values are selected appropriately in each step).

In [411] it is suggested to solve equation (4.49) only approximately, for instance, by some steps of minimal residual (MINRES) [350], with an appropriate preconditioner ${K}$ for $A-\theta_j^{(m)}I$, if available, but in fact any approximation technique for $t_j^{(m)}$ is formally allowed, provided that the projectors $(I-{u}_j^{(m)}{{u}_j^{(m)}}^{\ast})$ are taken into account. In our templates we will present ways to approximate $t_j^{(m)}$ with Krylov subspace methods.

We will now discuss how to use preconditioning for an iterative solver like generalized minimal residual (GMRES) or conjugate gradient squared (CGS), applied to equation (4.49). Suppose that we have a left preconditioner ${K}$ available for the operator $A-\theta_j^{(m)}I$, for which in some sense ${K}^{-1} (A-\theta_j^{(m)} I) \approx I$. Since $\theta_j^{(m)}$ varies with the iteration count ${m}$, so may the preconditioner, although it is often practical to work with the same ${K}$ for different values of $\theta$. Of course, the preconditioner ${K}$ has to be restricted to the subspace orthogonal to ${u}_j^{(m)}$ as well, which means that we have to work with, efficiently,

$$\widetilde{K}\equiv\left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right){K} \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right) .$$

This may seem unnecessarily complicated, and at first sight it also seems to involve a lot of overhead because of the projections $(I-{u}_j^{(m)}{{u}_j^{(m)}}^{\ast})$ surrounding the matrix-vector operations. But it all amounts to a handful of rather simple operations, as we will show now.

We assume that we use a Krylov solver with initial guess ${t}_0=0$ and with left preconditioning for the approximate solution of the correction equation (4.49). Since the starting vector is in the subspace orthogonal to ${u}_j^{(m)}$, all iteration vectors for the Krylov solver will be in that space. In that subspace we have to compute the vector ${z} \equiv \widetilde{K}^{-1}\widetilde{A}{v}$ for a vector ${v}$ supplied by the Krylov solver, and

$$\widetilde{A}\equiv \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\rig... ...\theta_j^{(m)} I) \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right).$$

We will do this in two steps. First we compute

$$\widetilde{A}v = \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right... ...\right){v} = \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right){y}$$

with $y \equiv (A-\theta_j^{(m)} I){v}$ since ${{u}_j^{(m)}}^\ast {v}=0$. Then, with left-preconditioning, we solve ${z}\perp {u}_j^{(m)}$ from

$$\widetilde{K} {z}= \left(I-{u}_j^{(m)}{{u}_j^{(m)}}^\ast\right){y} .$$

Since ${z}\perp {u}_j^{(m)}$, it follows that ${z}$ satisfies $K{z}={y}-\alpha {u}_j^{(m)}$ or ${z}=K^{-1}{y} - \alpha K^{-1}{u}_j^{(m)}$. The condition ${z}\perp {u}_j^{(m)}$ leads to

$$\alpha = \frac{{{u}_j^{(m)}}^\ast K^{-1}y} {{{u}_j^{(m)}}^\ast K^{-1}{u}_j^{(m)}} .$$

The vector $\widehat{y}\equiv {K}^{-1}{y}$ is solved from ${K}\widehat{y}={y}$ and, likewise, $\widehat{u}\equiv {K}^{-1}{u}_j^{(m)}$ is solved from ${K}\widehat{u}={u}_j^{(m)}$. The last equation has to be solved only once in an iteration process for equation (4.49), so that effectively ${i}_S+1$ operations with the preconditioner are required for ${i}_S$ iterations of the linear solver. Also, a matrix-vector multiplication with the left-preconditioned operator in an iteration of the Krylov solver requires only one inner product and one vector update instead of the four actions of the projector operator $(I-{u}_j^{(m)}{{u}_j^{(m)}}^{\ast})$. This has been worked out in the solution template, given in Algorithm 4.15. Along similar lines one can obtain an efficient template, although slightly more expensive than the left-preconditioned case, for the right-preconditioned operator. This template is described in Algorithm 4.16. For more details on preconditioning of the correction equation, see [412].

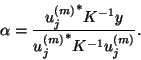
If we form an approximation for $t_j^{(m)}$ in (4.49) as $\widetilde{t}^{(m)}\equiv {K}^{-1}r -\alpha {K}^{-1} {u}_j^{(m)}$, with $\alpha$ such that $\widetilde{t}^{(m)}\perp {u}_j^{(m)}$ and without acceleration by an iterative solver, we obtain a process which was suggested by Olsen, Jørgensen, and Simons [344].