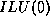 and
and 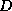 -
-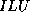
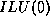 and
and 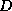 -
-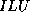
For the 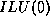 method, the incomplete factorization produces no
nonzero elements beyond the sparsity structure
of the original matrix, so that the preconditioner at worst
takes exactly as much space to store as the original matrix. In a
simplified version of
method, the incomplete factorization produces no
nonzero elements beyond the sparsity structure
of the original matrix, so that the preconditioner at worst
takes exactly as much space to store as the original matrix. In a
simplified version of 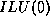 , called
, called 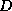 -
-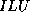 (Pommerell [174]), even less is needed. If not only we
prohibit fill-in elements, but we also alter only the diagonal
elements (that is, any alterations of off-diagonal elements are
ignored
(Pommerell [174]), even less is needed. If not only we
prohibit fill-in elements, but we also alter only the diagonal
elements (that is, any alterations of off-diagonal elements are
ignored![]() ),
we have the following situation.
),
we have the following situation.
Splitting the coefficient matrix into its diagonal, lower
triangular, and upper triangular parts as  , the
preconditioner can be written as
, the
preconditioner can be written as  where
where 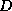 is the
diagonal matrix containing the pivots generated. Generating this
preconditioner is described in figure
is the
diagonal matrix containing the pivots generated. Generating this
preconditioner is described in figure ![]() .
.
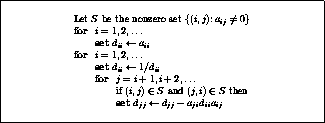
Figure: Construction of a 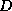 -
-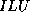 incomplete
factorization preconditioner, storing the inverses
of the pivots
incomplete
factorization preconditioner, storing the inverses
of the pivots
Since we use the
upper and lower triangle of the matrix unchanged, only storage space
for 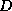 is needed. In fact, in order to avoid division operations
during the preconditioner solve stage we store
is needed. In fact, in order to avoid division operations
during the preconditioner solve stage we store 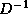 rather than
rather than 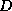 .
.
Remark: the resulting lower and upper factors of the preconditioner have
only nonzero elements in the set 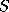 , but this fact is in general not
true for the preconditioner
, but this fact is in general not
true for the preconditioner 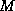 itself.
itself.
The fact that the 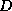 -
-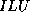 preconditioner contains the off-diagonal
parts of the original matrix was used by
Eisenstat [91] to derive at a more
efficient implementation of preconditioned CG. This new
implementation merges the application of the tridiagonal factors of
the matrix and the preconditioner, thereby saving a substantial number
of operations per iteration.
preconditioner contains the off-diagonal
parts of the original matrix was used by
Eisenstat [91] to derive at a more
efficient implementation of preconditioned CG. This new
implementation merges the application of the tridiagonal factors of
the matrix and the preconditioner, thereby saving a substantial number
of operations per iteration.