Footnotes
- ...\title
-
This work was supported in part by
DARPA and ARO under contract number DAAL03-91-C-0047,
the National Science Foundation Science and Technology Center Cooperative
Agreement No. CCR-8809615,
the Applied Mathematical Sciences subprogram of the Office of
Energy Research, U.S. Department of Energy, under Contract
DE-AC05-84OR21400,
and
the Stichting Nationale Computer Faciliteit (NCF) by Grant CRG 92.03.
- ...\author
- Los Alamos National Laboratory,
Los Alamos, NM 87544.
- ...\author
- Department of Computer Science, University of
Tennessee, Knoxville, TN 37996-1301.
- ...\author
- Applied Mathematics Department,
University of California, Los Angeles, CA 90024-1555.
- ...\author
- Computer Science Division and Mathematics
Department, University of California, Berkeley, CA 94720.
- ...\author
- Mathematical Sciences Section,
Oak Ridge National Laboratory, Oak Ridge, TN 37831-6367.
- ...\author
- National Institute of Standards and Technology,
Gaithersburg, MD, 20899
- ...\author
- Department of Mathematics, Utrecht University, Utrecht, the
Netherlands.
- ...
- For a discussion of BLAS as building
blocks, see [144][71][70][69] and
LAPACK routines [3]. Also, see
Appendix
 .
.
- ...
- For a more detailed account of the early
history of CG methods, we refer the reader to Golub and
O'Leary [108] and
Hestenes [123].
- ...
- Under certain conditions, one can show
that the point Jacobi algorithm is optimal, or close to optimal, in
the sense of reducing the condition number, among all
preconditioners of diagonal form. This was shown by Forsythe and
Strauss for matrices with Property A [99], and by van der
Sluis [198] for general sparse matrices. For
extensions to block Jacobi preconditioners, see
Demmel [66] and Elsner [95].
- ...
- The SOR and Gauss-Seidel matrices are never used as preconditioners,
for a rather technical reason.
SOR-preconditioning with optimal
 maps the eigenvalues of the
coefficient matrix to a circle in the complex plane;
see Hageman and Young [.3]HaYo:applied. In this case no
polynomial acceleration is possible, i.e., the accelerating polynomial
reduces to the trivial polynomial
maps the eigenvalues of the
coefficient matrix to a circle in the complex plane;
see Hageman and Young [.3]HaYo:applied. In this case no
polynomial acceleration is possible, i.e., the accelerating polynomial
reduces to the trivial polynomial  , and the resulting
method is simply the stationary SOR method.
Recent research by Eiermann and Varga [84] has shown
that polynomial
acceleration of SOR with suboptimal
, and the resulting
method is simply the stationary SOR method.
Recent research by Eiermann and Varga [84] has shown
that polynomial
acceleration of SOR with suboptimal  will yield no improvement
over simple SOR with optimal
will yield no improvement
over simple SOR with optimal  .
.
- ...
- To be precise, if we make an incomplete factorization
 , we
refer to positions in
, we
refer to positions in 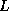 and
and 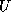 when we talk of positions in the
factorization. The matrix
when we talk of positions in the
factorization. The matrix 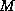 will have more nonzeros than
will have more nonzeros than 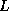 and
and 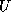 combined.
combined.
- ...
- The zero refers to the fact that only ``level zero'' fill is
permitted, that is, nonzero elements of the original matrix. Fill
levels are defined by calling an element of level
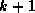 if it is
caused by elements at least one of which is of level
if it is
caused by elements at least one of which is of level  .
The first fill level is that caused by the original matrix elements.
.
The first fill level is that caused by the original matrix elements.
- ...
- In graph theoretical terms,
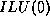 and
and 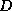 -
-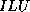 coincide if the matrix graph contains no triangles.
coincide if the matrix graph contains no triangles.
- ...
- Writing
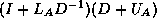 is equally valid, but in practice
harder to implement.
is equally valid, but in practice
harder to implement.
- ...
- On a machine with IEEE Standard
Floating Point Arithmetic,
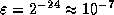 in single precision, and
in single precision, and  in double precision.
in double precision.
- ...
- IEEE standard
floating point arithmetic permits computations with
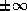 and
NaN, or Not-a-Number, symbols.
and
NaN, or Not-a-Number, symbols.
- ...
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 maps the eigenvalues of the
coefficient matrix to a circle in the complex plane;
see Hageman and Young [.3]HaYo:applied. In this case no
polynomial acceleration is possible, i.e., the accelerating polynomial
reduces to the trivial polynomial
maps the eigenvalues of the
coefficient matrix to a circle in the complex plane;
see Hageman and Young [.3]HaYo:applied. In this case no
polynomial acceleration is possible, i.e., the accelerating polynomial
reduces to the trivial polynomial  , and the resulting
method is simply the stationary SOR method.
Recent research by Eiermann and Varga [84] has shown
that polynomial
acceleration of SOR with suboptimal
, and the resulting
method is simply the stationary SOR method.
Recent research by Eiermann and Varga [84] has shown
that polynomial
acceleration of SOR with suboptimal  will yield no improvement
over simple SOR with optimal
will yield no improvement
over simple SOR with optimal  .
. , we
refer to positions in
, we
refer to positions in 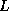 and
and 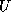 when we talk of positions in the
factorization. The matrix
when we talk of positions in the
factorization. The matrix 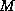 will have more nonzeros than
will have more nonzeros than 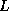 and
and 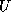 combined.
combined.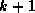 if it is
caused by elements at least one of which is of level
if it is
caused by elements at least one of which is of level  .
The first fill level is that caused by the original matrix elements.
.
The first fill level is that caused by the original matrix elements.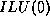 and
and 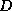 -
-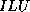 coincide if the matrix graph contains no triangles.
coincide if the matrix graph contains no triangles.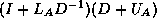 is equally valid, but in practice
harder to implement.
is equally valid, but in practice
harder to implement.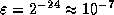 in single precision, and
in single precision, and  in double precision.
in double precision.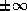 and
NaN, or Not-a-Number, symbols.
and
NaN, or Not-a-Number, symbols.