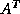 instead of
instead of 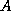 . Thus we update two sequences of
residuals
. Thus we update two sequences of
residuals
The Conjugate Gradient method is not suitable for nonsymmetric systems because the residual vectors cannot be made orthogonal with short recurrences (for proof of this see Voevodin [213] or Faber and Manteuffel [96]). The GMRES method retains orthogonality of the residuals by using long recurrences, at the cost of a larger storage demand. The BiConjugate Gradient method takes another approach, replacing the orthogonal sequence of residuals by two mutually orthogonal sequences, at the price of no longer providing a minimization.
The update relations for residuals in the Conjugate Gradient method
are augmented in the BiConjugate Gradient method by relations
that are similar
but based on 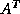 instead of
instead of 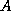 . Thus we update two sequences of
residuals
. Thus we update two sequences of
residuals
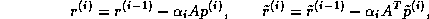
and two sequences of search directions
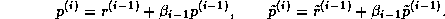
The choices

ensure the bi-orthogonality relations
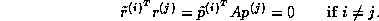
The pseudocode for the Preconditioned BiConjugate Gradient
Method with preconditioner 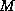 is given in Figure
is given in Figure ![]() .
.

Figure: The Preconditioned BiConjugate Gradient Method