Implementation





Next: BiConjugate Gradient (BiCG)
Up: Generalized Minimal Residual
Previous: Theory
A common implementation of GMRES
is suggested by Saad and Schultz in [189] and
relies on using modified Gram-Schmidt orthogonalization. Householder
transformations, which are relatively costly but stable, have also
been proposed. The Householder approach results in a three-fold
increase in work associated with inner products and
vector updates (not with matrix vector products);
however, convergence may be better, especially for
ill-conditioned systems
(see Walker [214]). From
the point of view of parallelism , Gram-Schmidt orthogonalization may be
preferred, giving up some stability for better parallelization
properties (see Demmel, Heath and Van der Vorst [67]).
Here we adopt the Modified Gram-Schmidt approach.
The major drawback to GMRES is that the amount of work and storage
required per iteration rises linearly with the iteration count.
Unless one is fortunate enough to obtain extremely fast convergence,
the cost will rapidly become prohibitive. The usual way to overcome
this limitation is by restarting the iteration. After a chosen number
(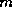 ) of iterations, the accumulated data are cleared and the
intermediate results are used as the initial data for the next
) of iterations, the accumulated data are cleared and the
intermediate results are used as the initial data for the next
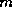 iterations. This procedure is repeated until convergence is
achieved. The difficulty is in choosing an appropriate value for
iterations. This procedure is repeated until convergence is
achieved. The difficulty is in choosing an appropriate value for 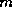 .
If
.
If 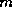 is ``too small'', GMRES(
is ``too small'', GMRES(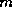 ) may be slow to converge, or fail
to converge entirely. A value of
) may be slow to converge, or fail
to converge entirely. A value of 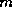 that is larger than necessary
involves excessive work (and uses more storage). Unfortunately, there
are no definite rules governing the choice of
that is larger than necessary
involves excessive work (and uses more storage). Unfortunately, there
are no definite rules governing the choice of 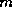 -choosing when to
restart is a matter of experience.
-choosing when to
restart is a matter of experience.
For a discussion of GMRES for vector and shared memory computers see
Dongarra et al. [71]; for more general
architectures,
see Demmel, Heath and Van der Vorst [67] .
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
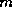 ) of iterations, the accumulated data are cleared and the
intermediate results are used as the initial data for the next
) of iterations, the accumulated data are cleared and the
intermediate results are used as the initial data for the next
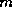 iterations. This procedure is repeated until convergence is
achieved. The difficulty is in choosing an appropriate value for
iterations. This procedure is repeated until convergence is
achieved. The difficulty is in choosing an appropriate value for 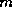 .
If
.
If 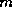 is ``too small'', GMRES(
is ``too small'', GMRES(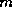 ) may be slow to converge, or fail
to converge entirely. A value of
) may be slow to converge, or fail
to converge entirely. A value of 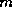 that is larger than necessary
involves excessive work (and uses more storage). Unfortunately, there
are no definite rules governing the choice of
that is larger than necessary
involves excessive work (and uses more storage). Unfortunately, there
are no definite rules governing the choice of 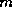 -choosing when to
restart is a matter of experience.
-choosing when to
restart is a matter of experience.